1971. 寻找图中是否存在路径

题目链接

有一个具有 n 个顶点的双向图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。每个顶点对由最多一条边连接，并且没有顶点存在与自身相连的边。

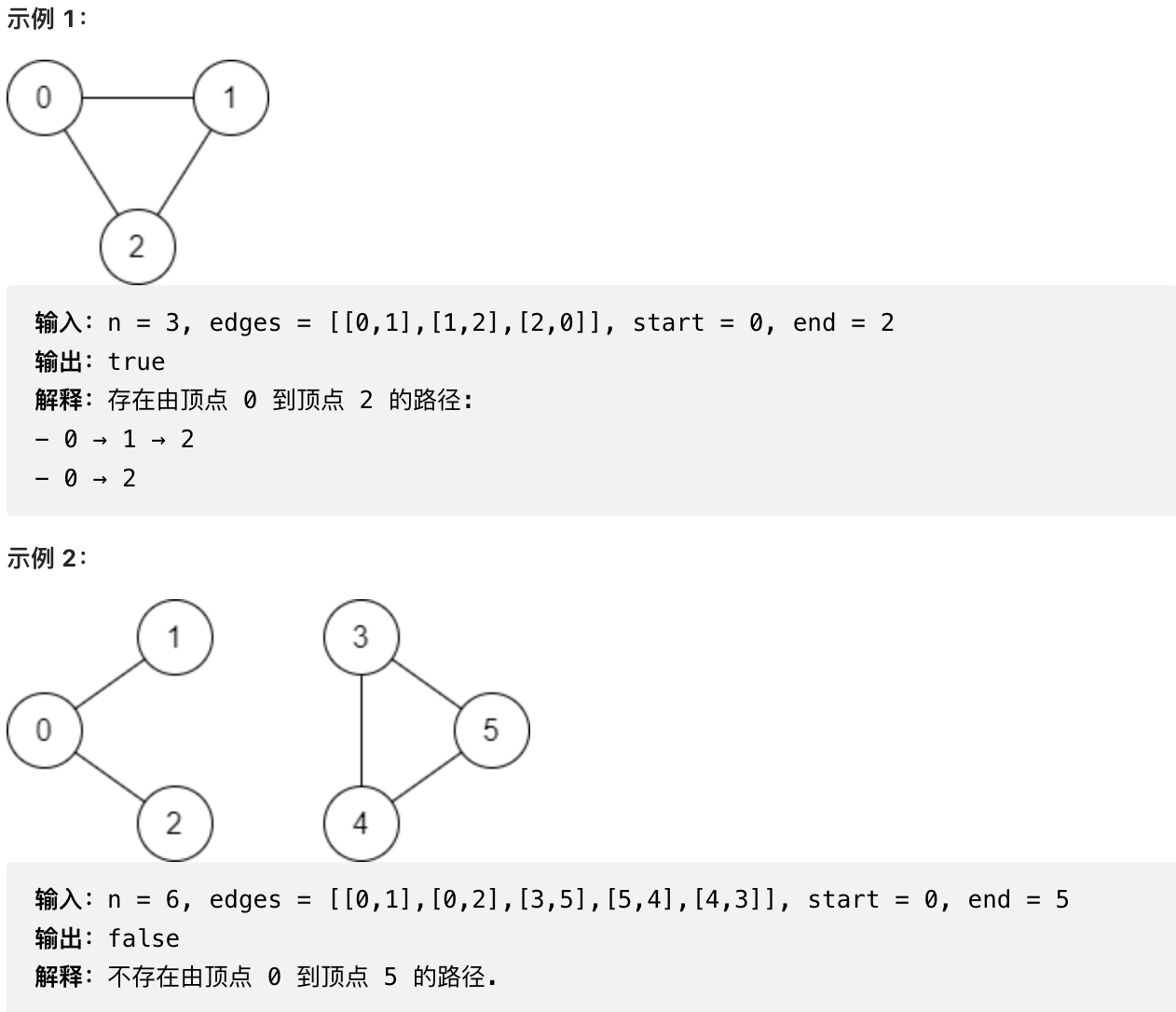
请你确定是否存在从顶点 start 开始，到顶点 end 结束的有效路径。

给你数组 edges 和整数 n、start 和 end，如果从 start 到 end 存在有效路径，则返回 true，否则返回 false 。

提示:

1 <= n <= 2 * 10^5
0 <= edges.length <= 2 * 10^5
edges[i].length == 2
0 <= ui, vi <= n - 1
ui != vi
0 <= start, end <= n - 1
不存在双向边
不存在指向顶点自身的边

思路

本题是并查集基础题目。如果还不了解并查集，可以看这里：并查集理论基础

并查集可以解决什么问题呢？

主要就是集合问题，两个节点在不在一个集合，也可以将两个节点添加到一个集合中。

这里整理出我的并查集模板如下：

int n = 1005; // n根据题目中节点数量而定，一般比节点数量大一点就好
vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

// 并查集初始化
void init() {
    for (int i = 0; i < n; ++i) {
        father[i] = i;
    }
}
// 并查集里寻根的过程
int find(int u) {
    return u == father[u] ? u : father[u] = find(father[u]); // 路径压缩
}

// 判断 u 和 v是否找到同一个根
bool isSame(int u, int v) {
    u = find(u);
    v = find(v);
    return u == v;
}

// 将v->u 这条边加入并查集
void join(int u, int v) {
    u = find(u); // 寻找u的根
    v = find(v); // 寻找v的根
    if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
    father[v] = u;
}

以上模板中，只要修改 n 大小就可以，本题 n 不会超过 2 * 10^5。

并查集主要有三个功能。

寻找根节点，函数：find(int u)，也就是判断这个节点的祖先节点是哪个
将两个节点接入到同一个集合，函数：join(int u, int v)，将两个节点连在同一个根节点上
判断两个节点是否在同一个集合，函数：isSame(int u, int v)，就是判断两个节点是不是同一个根节点

简单介绍并查集之后，我们再来看一下这道题目。

为什么说这道题目是并查集基础题目，题目中各个点是双向图链接，那么判断一个顶点到另一个顶点有没有有效路径其实就是看这两个顶点是否在同一个集合里。

如何算是同一个集合呢，有边连在一起，就算是一个集合。

此时我们就可以直接套用并查集模板。

使用 join(int u, int v)将每条边加入到并查集。

最后 isSame(int u, int v) 判断是否是同一个根就可以了。

C++代码如下：

class Solution {
private:
    int n = 200005; // 节点数量 20000
    vector<int> father = vector<int> (n, 0); // C++里的一种数组结构

    // 并查集初始化
    void init() {
        for (int i = 0; i < n; ++i) { father[i] = i;
        }
    }
    // 并查集里寻根的过程
    int find(int u) {
        return u == father[u] ? u : father[u] = find(father[u]);
    }

    // 判断 u 和 v是否找到同一个根
    bool isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    // 将v->u 这条边加入并查集
    void join(int u, int v) {
        u = find(u); // 寻找u的根
        v = find(v); // 寻找v的根
        if (u == v) return ; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
        father[v] = u;
    }

public:
    bool validPath(int n, vector<vector<int>>& edges, int source, int destination) {
        init();
        for (int i = 0; i < edges.size(); i++) {
            join(edges[i][0], edges[i][1]);
        }
        return isSame(source, destination);

    }
};

其他语言版本

Java：

class Solution {

    int[] father;
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        father = new int[n];
        init();
        for (int i = 0; i < edges.length; i++) {
            join(edges[i][0], edges[i][1]);
        }

        return isSame(source, destination);
    }

    // 并查集初始化
    public void init() {
        for (int i = 0; i < father.length; i++) {
            father[i] = i;
        }
    }

    // 并查集里寻根的过程
    public int find(int u) {
        if (u == father[u]) {
            return u;
        } else {
            father[u] = find(father[u]);
            return father[u];
        }
    }

    // 判断 u 和 v是否找到同一个根
    public boolean isSame(int u, int v) {
        u = find(u);
        v = find(v);
        return u == v;
    }

    // 将v->u 这条边加入并查集
    public void join(int u, int v) {
        u = find(u); // 寻找u的根
        v = find(v); // 寻找v的根
        if (u == v) return; // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回

        father[v] = u;
    }

}

Python：

PYTHON 并查集解法如下：

class Solution:
    def validPath(self, n: int, edges: List[List[int]], source: int, destination: int) -> bool:
        p = [i for i in range(n)]
        def find(i):
            if p[i] != i:
                p[i] = find(p[i])
            return p[i]
        for u, v in edges:
            p[find(u)] = find(v)
        return find(source) == find(destination)

Javascript：

Javascript 并查集解法如下：

class unionF{
    constructor(n){
        this.count = n
        this.roots = new Array(n).fill(0).map((item,index)=>index)
    }

    findRoot(x){
        if(this.roots[x]!==x){
            this.roots[x] = this.findRoot(this.roots[x])
        }
        return this.roots[x]
    }

    union(x,y){
        const rx = this.findRoot(x)
        const ry = this.findRoot(y)
        this.roots[rx] = ry
        this.count--
    }

    isConnected(x,y){
        return this.findRoot(x)===this.findRoot(y)
    }
}

var validPath = function(n, edges, source, destination) {
    const UF = new unionF(n)
    for(const [s,t] of edges){
        UF.union(s,t)
    }
    return UF.isConnected(source,destination)
};

Javascript 双向 bfs 解法如下：

var validPath = function(n, edges, source, destination) {
    const graph = new Array(n).fill(0).map(()=>[])
    for(const [s,t] of edges){
        graph[s].push(t)
        graph[t].push(s)
    }

    const visited = new Array(n).fill(false)
    function bfs(start,end,graph){
        const startq = [start]
        const endq = [end]
        while(startq.length&&endq.length){
            const slen = startq.length
            for(let i = 0;i<slen;i++){
                const scur = startq.shift()
                if(visited[scur]) continue
                if(endq.includes(scur)) return true
                visited[scur] = true
                const neighbors = graph[scur]
                startq.push(...neighbors)
            }

            const elen = endq.length
            for(let i = 0;i<elen;i++){
                const ecur = endq.shift()
                if(visited[ecur]) continue
                if(startq.includes(ecur)) return true
                visited[ecur] = true
                const neighbors = graph[ecur]
                endq.push(...neighbors)
            }
        }
        return false
    }
    return bfs(source,destination,graph)
};

1971.寻找图中是否存在路径

1971. 寻找图中是否存在路径

思路

其他语言版本

Java：

Python：

Javascript：