941.有效的山脉数组

力扣题目链接

给定一个整数数组 arr，如果它是有效的山脉数组就返回 true，否则返回 false。

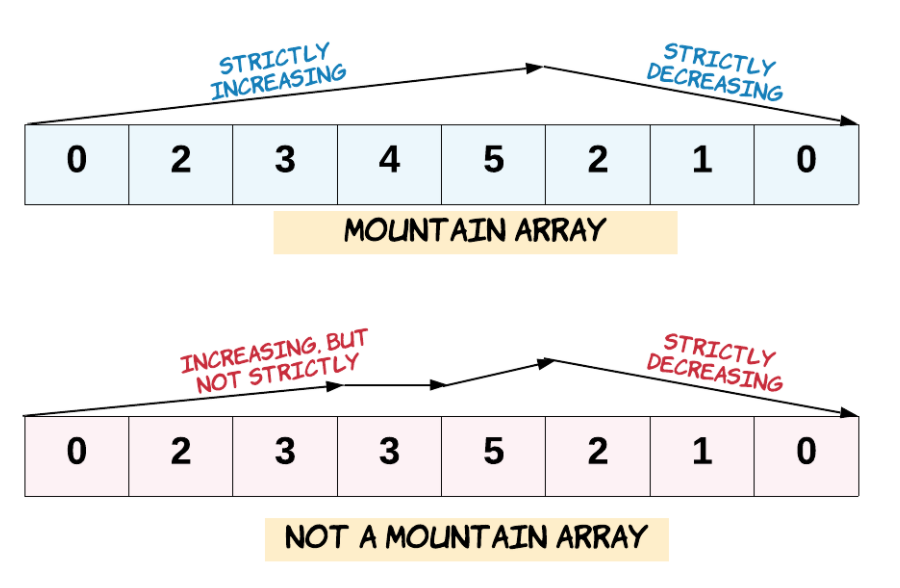
让我们回顾一下，如果 A 满足下述条件，那么它是一个山脉数组：

arr.length >= 3
在 0 < i < arr.length - 1 条件下，存在 i 使得：
- arr[0] < arr[1] < ... arr[i-1] < arr[i]
- arr[i] > arr[i+1] > ... > arr[arr.length - 1]

示例 1：

输入：arr = [2,1]
输出：false

示例 2：

输入：arr = [3,5,5]
输出：false

示例 3：

输入：arr = [0,3,2,1]
输出：true

思路

判断是山峰，主要就是要严格的保存左边到中间，和右边到中间是递增的。

这样可以使用两个指针，left和right，让其按照如下规则移动，如图：

注意这里还是有一些细节，例如如下两点：

因为left和right是数组下标，移动的过程中注意不要数组越界
如果left或者right没有移动，说明是一个单调递增或者递减的数组，依然不是山峰

C++代码如下：

class Solution {
public:
    bool validMountainArray(vector<int>& A) {
        if (A.size() < 3) return false;
        int left = 0;
        int right = A.size() - 1;

        // 注意防止越界
        while (left < A.size() - 1 && A[left] < A[left + 1]) left++;

        // 注意防止越界
        while (right > 0 && A[right] < A[right - 1]) right--;

        // 如果left或者right都在起始位置，说明不是山峰
        if (left == right && left != 0 && right != A.size() - 1) return true;
        return false;
    }
};

如果想系统学一学双指针的话，可以看一下这篇双指针法：总结篇！

其他语言版本

Java

class Solution {
    public boolean validMountainArray(int[] arr) {
        if (arr.length < 3) { // 此时，一定不是有效的山脉数组
            return false;
        }
        // 双指针
        int left = 0;
        int right = arr.length - 1;
        // 注意防止指针越界
        while (left + 1 < arr.length && arr[left] < arr[left + 1]) {
            left++;
        }
        // 注意防止指针越界
        while (right > 0 && arr[right] < arr[right - 1]) {
            right--;
        }
        // 如果left或者right都在起始位置，说明不是山峰
        if (left == right && left != 0 && right != arr.length - 1) {
            return true;
        }
        return false;
    }
}

Python3

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        left, right = 0, len(arr)-1
        
        while left < len(arr)-1 and arr[left+1] > arr[left]:
            left += 1
        
        while right > 0 and arr[right-1] > arr[right]:
            right -= 1
        
        return left == right and right != 0 and left != len(arr)-1

Go

func validMountainArray(arr []int) bool {
	if len(arr) < 3 {
		return false
	}

	i := 1
	flagIncrease := false // 上升
	flagDecrease := false // 下降

	for ; i < len(arr) && arr[i-1] < arr[i]; i++ {
		flagIncrease = true;
	}

	for ; i < len(arr) && arr[i-1] > arr[i]; i++ {
		flagDecrease = true;
	}

	return i == len(arr) && flagIncrease && flagDecrease;
}

JavaScript

var validMountainArray = function(arr) {
    if(arr.length < 3) return false;// 一定不是山脉数组
    let left = 0, right = arr.length - 1;// 双指针
    // 注意防止越界
    while(left < arr.length && arr[left] < arr[left+1]) left++;
    while(right>0 && arr[right-1] > arr[right]) right--;
    // 如果left或者right都在起始位置，说明不是山峰
    if(left === right && left !== 0 && right !== arr.length - 1) return true;
    return false;
};

TypeScript

function validMountainArray(arr: number[]): boolean {
    const length: number = arr.length;
    if (length < 3) return false;
    let left: number = 0,
        right: number = length - 1;
    while (left < (length - 1) && arr[left] < arr[left + 1]) {
        left++;
    }
    while (right > 0 && arr[right] < arr[right - 1]) {
        right--;
    }
    if (left === right && left !== 0 && right !== length - 1)
        return true;
    return false;
};

C#

public class Solution {
    public bool ValidMountainArray(int[] arr) {
        if (arr.Length < 3) return false;

        int left = 0;
        int right = arr.Length - 1;

        while (left + 1< arr.Length && arr[left] < arr[left + 1]) left ++;
        while (right > 0 && arr[right] < arr[right - 1]) right --;
        if (left == right && left != 0 && right != arr.Length - 1) return true;
	
        return false;
    }
}

0941.有效的山脉数组