746. 使用最小花费爬楼梯

力扣题目链接

旧题目描述：

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。

每当你爬上一个阶梯你都要花费对应的体力值，一旦支付了相应的体力值，你就可以选择向上爬一个阶梯或者爬两个阶梯。

请你找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

示例 1：

输入：cost = [10, 15, 20]
输出：15
解释：最低花费是从 cost[1] 开始，然后走两步即可到阶梯顶，一共花费 15 。

示例 2：

输入：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出：6
解释：最低花费方式是从 cost[0] 开始，逐个经过那些 1 ，跳过 cost[3] ，一共花费 6 。

提示：

cost 的长度范围是 [2, 1000]。
cost[i] 将会是一个整型数据，范围为 [0, 999] 。

本题之前的题目描述是很模糊的，看不出来，第一步需要花费体力值，最后一步不用花费，还是说第一步不花费体力值，最后一步花费。

后来力扣改了题目描述，新题目描述：

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

请你计算并返回达到楼梯顶部的最低花费。

思路

（在力扣修改了题目描述下，我又重新修改了题解）

修改之后的题意就比较明确了，题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于跳到下标 0 或者下标 1 是不花费体力的，从下标 0 下标1 开始跳就要花费体力了。

确定dp数组以及下标的含义

使用动态规划，就要有一个数组来记录状态，本题只需要一个一维数组dp[i]就可以了。

dp[i]的定义：到达第i台阶所花费的最少体力为dp[i]。

对于dp数组的定义，大家一定要清晰！

确定递推公式

可以有两个途径得到dp[i]，一个是dp[i-1] 一个是dp[i-2]。

dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。

dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。

那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢？

一定是选最小的，所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);

dp数组如何初始化

看一下递归公式，dp[i]由dp[i - 1]，dp[i - 2]推出，既然初始化所有的dp[i]是不可能的，那么只初始化dp[0]和dp[1]就够了，其他的最终都是dp[0]dp[1]推出。

那么 dp[0] 应该是多少呢？根据dp数组的定义，到达第0台阶所花费的最小体力为dp[0]，那么有同学可能想，那dp[0] 应该是 cost[0]，例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话，dp[0] 就是 cost[0] 应该是1。

这里就要说明本题力扣为什么改题意，而且修改题意之后就清晰很多的原因了。

新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说到达第 0 个台阶是不花费的，但从第0 个台阶往上跳的话，需要花费 cost[0]。

所以初始化 dp[0] = 0，dp[1] = 0;

确定遍历顺序

最后一步，递归公式有了，初始化有了，如何遍历呢？

本题的遍历顺序其实比较简单，简单到很多同学都忽略了思考这一步直接就把代码写出来了。

因为是模拟台阶，而且dp[i]由dp[i-1]dp[i-2]推出，所以是从前到后遍历cost数组就可以了。

但是稍稍有点难度的动态规划，其遍历顺序并不容易确定下来。
例如：01背包，都知道两个for循环，一个for遍历物品嵌套一个for遍历背包容量，那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢？以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢？

这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的！

举例推导dp数组

拿示例2：cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ，来模拟一下dp数组的状态变化，如下：

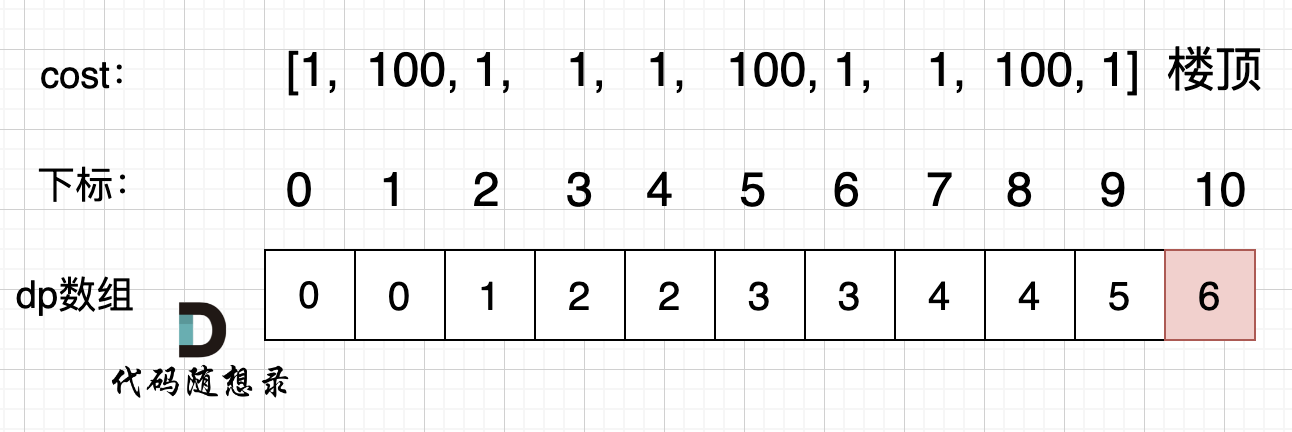
如果大家代码写出来有问题，就把dp数组打印出来，看看和如上推导的是不是一样的。

以上分析完毕，整体C++代码如下：

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size() + 1);
        dp[0] = 0; // 默认第一步都是不花费体力的
        dp[1] = 0;
        for (int i = 2; i <= cost.size(); i++) {
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[cost.size()];
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

还可以优化空间复杂度，因为dp[i]就是由前两位推出来的，那么也不用dp数组了，C++代码如下：

// 版本二
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dp0 = 0;
        int dp1 = 0;
        for (int i = 2; i <= cost.size(); i++) {
            int dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2]);
            dp0 = dp1; // 记录一下前两位
            dp1 = dpi;
        }
        return dp1;
    }
};

时间复杂度：O(n)
空间复杂度：O(1)

当然如果在面试中，能写出版本一就行，除非面试官额外要求空间复杂度，那么再去思考版本二，因为版本二还是有点绕。版本一才是正常思路。

拓展

旧力扣描述，如果按照第一步是花费的，最后一步不花费，那么代码是这么写的，提交也可以通过

// 版本一
class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        vector<int> dp(cost.size());
        dp[0] = cost[0]; // 第一步有花费
        dp[1] = cost[1];
        for (int i = 2; i < cost.size(); i++) {
            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        // 注意最后一步可以理解为不用花费，所以取倒数第一步，第二步的最少值
        return min(dp[cost.size() - 1], dp[cost.size() - 2]);
    }
};

当然如果对动态规划理解不够深入的话，拓展内容就别看了，容易越看越懵。

总结

大家可以发现这道题目相对于昨天的动态规划：爬楼梯又难了一点，但整体思路是一样的。

从动态规划：斐波那契数到动态规划：爬楼梯再到今天这道题目，录友们感受到循序渐进的梯度了嘛。

每个系列开始的时候，都有录友和我反馈说题目太简单了，赶紧上难度，但也有录友和我说有点难了，快跟不上了。

其实我选的题目都是有目的性的，就算是简单题，也是为了练习方法论，然后难度都是梯度上来的，一环扣一环。

但我也可以随便选来一道难题讲呗，这其实是最省事的，不用管什么题目顺序，看心情找一道就讲。

难的是把题目按梯度排好，循序渐进，再按照统一方法论把这些都串起来，所以大家不要催我哈，按照我的节奏一步一步来就行了。

其他语言版本

以下版本其他语言版本，大多是按照旧力扣题解来写的，欢迎大家在Github上提交pr，修正一波。

Java

// 方式一：第一步不支付费用
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int len = cost.length;
        int[] dp = new int[len + 1];

        // 从下标为 0 或下标为 1 的台阶开始，因此支付费用为0
        dp[0] = 0;
        dp[1] = 0;

        // 计算到达每一层台阶的最小费用
        for (int i = 2; i <= len; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }

        return dp[len];
    }
}

// 方式二：第一步支付费用
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        //最后一步，如果是由倒数第二步爬，则最后一步的体力花费可以不用算
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
    }
}

Python

动态规划（版本一）


class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp = [0] * (len(cost) + 1)
        dp[0] = 0  # 初始值，表示从起点开始不需要花费体力
        dp[1] = 0  # 初始值，表示经过第一步不需要花费体力
        
        for i in range(2, len(cost) + 1):
            # 在第i步，可以选择从前一步（i-1）花费体力到达当前步，或者从前两步（i-2）花费体力到达当前步
            # 选择其中花费体力较小的路径，加上当前步的花费，更新dp数组
            dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
        
        return dp[len(cost)]  # 返回到达楼顶的最小花费

动态规划（版本二）

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp0 = 0  # 初始值，表示从起点开始不需要花费体力
        dp1 = 0  # 初始值，表示经过第一步不需要花费体力
        
        for i in range(2, len(cost) + 1):
            # 在第i步，可以选择从前一步（i-1）花费体力到达当前步，或者从前两步（i-2）花费体力到达当前步
            # 选择其中花费体力较小的路径，加上当前步的花费，得到当前步的最小花费
            dpi = min(dp1 + cost[i - 1], dp0 + cost[i - 2])
            
            dp0 = dp1  # 更新dp0为前一步的值，即上一次循环中的dp1
            dp1 = dpi  # 更新dp1为当前步的最小花费
        
        return dp1  # 返回到达楼顶的最小花费

动态规划（版本三）

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp = [0] * len(cost)
        dp[0] = cost[0]  # 第一步有花费
        dp[1] = cost[1]
        for i in range(2, len(cost)):
            dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
        # 注意最后一步可以理解为不用花费，所以取倒数第一步，第二步的最少值
        return min(dp[-1], dp[-2])

动态规划（版本四）

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        n = len(cost)
        prev_1 = cost[0]  # 前一步的最小花费
        prev_2 = cost[1]  # 前两步的最小花费
        for i in range(2, n):
            current = min(prev_1, prev_2) + cost[i]  # 当前位置的最小花费
            prev_1, prev_2 = prev_2, current  # 更新前一步和前两步的最小花费
        return min(prev_1, prev_2)  # 最后一步可以理解为不用花费，取倒数第一步和第二步的最少值

Go

func minCostClimbingStairs(cost []int) int {
    f := make([]int, len(cost) + 1)
    f[0], f[1] = 0, 0
    for i := 2; i <= len(cost); i++ {
        f[i] = min(f[i-1] + cost[i-1], f[i-2] + cost[i-2])
    }
    return f[len(cost)]
}
func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

第二种思路: dp[i]表示从i层起跳所需要支付的最小费用
递推公式:
i<n :dp[i] = min(dp[i-1],dp[i-2])+cost[i]
i==n:dp[i] = min(dp[i-1],dp[i-2]) (登顶)

func minCostClimbingStairs(cost []int) int {
	n := len(cost)
	dp := make([]int, n+1)
	dp[0], dp[1] = cost[0], cost[1]
	for i := 2; i <= n; i++ {
		if i < n {
			dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
		} else {
			dp[i] = min(dp[i-1], dp[i-2])
		}
	}
	return dp[n]
}
func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

JavaScript

var minCostClimbingStairs = function(cost) {
  const dp = [0, 0]
  for (let i = 2; i <= cost.length; ++i) {
    dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
  }
  return dp[cost.length]
};

不使用 dp 数组

var minCostClimbingStairs = function(cost) {
  let dpBefore = 0,
    dpAfter = 0
    for(let i = 2;i <= cost.length;i++){
        let dpi = Math.min(dpBefore + cost[i - 2],dpAfter + cost[i - 1])
        dpBefore = dpAfter
        dpAfter = dpi
    }
    return dpAfter
};

TypeScript

function minCostClimbingStairs(cost: number[]): number {
  const dp = [0, 0]
  for (let i = 2; i <= cost.length; i++) {
    dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
  }
  return dp[cost.length]
}

不使用 dp 数组

function minCostClimbingStairs(cost: number[]): number {
  let dpBefore = 0,
    dpAfter = 0
  for (let i = 2; i <= cost.length; i++) {
    let dpi = Math.min(dpBefore + cost[i - 2], dpAfter + cost[i - 1])
    dpBefore = dpAfter
    dpAfter = dpi
  }
  return dpAfter
}

Rust

impl Solution {
    pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
        let mut dp = vec![0; cost.len() + 1];
        for i in 2..=cost.len() {
            dp[i] = (dp[i - 1] + cost[i - 1]).min(dp[i - 2] + cost[i - 2]);
        }
        dp[cost.len()]
    }
}

不使用 dp 数组

impl Solution {
    pub fn min_cost_climbing_stairs(cost: Vec<i32>) -> i32 {
        let (mut dp_before, mut dp_after) = (0, 0);
        for i in 2..=cost.len() {
            let dpi = (dp_before + cost[i - 2]).min(dp_after + cost[i - 1]);
            dp_before = dp_after;
            dp_after = dpi;
        }
        dp_after
    }
}

C

#include <math.h>
int minCostClimbingStairs(int *cost, int costSize) {
  int dp[costSize + 1];
  dp[0] = dp[1] = 0;
  for (int i = 2; i <= costSize; i++) {
    dp[i] = fmin(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);
  }
  return dp[costSize];
}

不使用 dp 数组

#include <math.h>
int minCostClimbingStairs(int *cost, int costSize) {
  int dpBefore = 0, dpAfter = 0;
  for (int i = 2; i <= costSize; i++) {
    int dpi = fmin(dpBefore + cost[i - 2], dpAfter + cost[i - 1]);
    dpBefore = dpAfter;
    dpAfter = dpi;
  }
  return dpAfter;
}

Scala

object Solution {
  def minCostClimbingStairs(cost: Array[Int]): Int = {
    var dp = new Array[Int](cost.length)
    dp(0) = cost(0)
    dp(1) = cost(1)
    for (i <- 2 until cost.length) {
      dp(i) = math.min(dp(i - 1), dp(i - 2)) + cost(i)
    }
    math.min(dp(cost.length - 1), dp(cost.length - 2))
  }
}

第二种思路: dp[i] 表示爬到第i-1层所需的最小花费，状态转移方程为: dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

object Solution {
  def minCostClimbingStairs(cost: Array[Int]): Int = {
    var dp = new Array[Int](cost.length + 1)
    for (i <- 2 until cost.length + 1) {
      dp(i) = math.min(dp(i - 1) + cost(i - 1), dp(i - 2) + cost(i - 2))
    }
    dp(cost.length)
  }
}

C#

public class Solution
{
    public int MinCostClimbingStairs(int[] cost)
    {
        int[] dp=new int[2] { cost[0], cost[1] };
        for (int i = 2; i < cost.Length; i++)
        {
            int temp = Math.Min(dp[0], dp[1])+cost[i];
            dp[0]=dp[1];
            dp[1]=temp;
        }
        return Math.Min(dp[0],dp[1]);
    }
}

0746.使用最小花费爬楼梯

746. 使用最小花费爬楼梯

思路

拓展

总结

其他语言版本

Java

Python

Go

JavaScript

TypeScript

Rust

C

Scala

C#