1791.找出星型图的中心节点

题目链接

本题思路就是统计各个节点的度（这里没有区别入度和出度），如果某个节点的度等于这个图边的数量。 那么这个节点一定是中心节点。

什么是度，可以理解为，链接节点的边的数量。 题目中度如图所示：

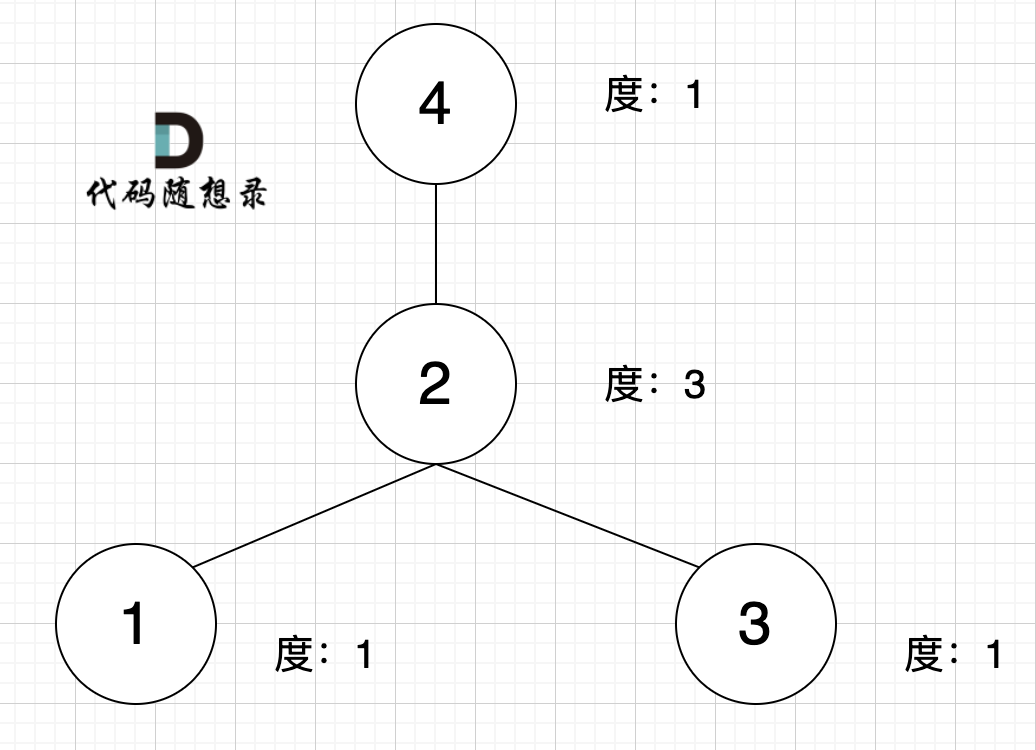
至于出度和入度，那就是在有向图里的概念了，本题是无向图。

本题代码如下：

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        unordered_map<int ,int> du;
        for (int i = 0; i < edges.size(); i++) { // 统计各个节点的度    
                du[edges[i][1]]++;
                du[edges[i][0]]++;
        }
        unordered_map<int, int>::iterator iter;  // 找出度等于边熟练的节点
        for (iter = du.begin(); iter != du.end(); iter++) { 
            if (iter->second == edges.size()) return iter->first;
        }
        return -1;
    }
};

其实可以只记录度不用最后统计，因为题目说了一定是星状图，所以 一旦有 节点的度 大于1，就返回该节点数值就行，只有中心节点的度会大于1。

代码如下：

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        vector<int> du(edges.size() + 2);  // edges.size() + 1 为节点数量，下标表示节点数，所以+2 
        for (int i = 0; i < edges.size(); i++) {
            du[edges[i][1]]++;
            du[edges[i][0]]++;
            if (du[edges[i][1]] > 1) return edges[i][1];
            if (du[edges[i][0]] > 1) return edges[i][0];

        }
        return -1;
    }
};

以上代码中没有使用 unordered_map，因为遍历的时候，开辟新空间会浪费时间，而采用 vector，这是 空间换时间的一种策略。

代码其实可以再精简：

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        vector<int> du(edges.size() + 2);
        for (int i = 0; i < edges.size(); i++) {
            if (++du[edges[i][1]] > 1) return edges[i][1];
            if (++du[edges[i][0]] > 1) return edges[i][0];
        }
        return -1;
    }
};