132. 分割回文串 II

力扣题目链接

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是回文。

返回符合要求的最少分割次数。

示例 1：

输入：s = "aab"
输出：1
解释：只需一次分割就可将 s 分割成 ["aa","b"] 这样两个回文子串。

示例 2：
输入：s = "a"
输出：0

示例 3：
输入：s = "ab"
输出：1

提示：

1 <= s.length <= 2000
s 仅由小写英文字母组成

思路

我们在讲解回溯法系列的时候，讲过了这道题目回溯算法：131.分割回文串。

本题呢其实也可以使用回溯法，只不过会超时！（通过记忆化回溯，也可以过，感兴趣的同学可以自行研究一下）

我们来讲一讲如何使用动态规划，来解决这道题目。

关于回文子串，两道题目题目大家是一定要掌握的。

动态规划：647. 回文子串
5.最长回文子串和 647.回文子串基本一样的

这两道题目是回文子串的基础题目，本题也要用到相关的知识点。

动规五部曲分析如下：

确定dp数组（dp table）以及下标的含义

dp[i]：范围是[0, i]的回文子串，最少分割次数是dp[i]。

确定递推公式

来看一下由什么可以推出dp[i]。

如果要对长度为[0, i]的子串进行分割，分割点为j。

那么如果分割后，区间[j + 1, i]是回文子串，那么dp[i] 就等于 dp[j] + 1。

这里可能有同学就不明白了，为什么只看[j + 1, i]区间，不看[0, j]区间是不是回文子串呢？

那么在回顾一下dp[i]的定义：范围是[0, i]的回文子串，最少分割次数是dp[i]。

[0, j]区间的最小切割数量，我们已经知道了就是dp[j]。

此时就找到了递推关系，当切割点j在[0, i] 之间时候，dp[i] = dp[j] + 1;

本题是要找到最少分割次数，所以遍历j的时候要取最小的dp[i]。

所以最后递推公式为：dp[i] = min(dp[i], dp[j] + 1);

注意这里不是要 dp[j] + 1 和 dp[i]去比较，而是要在遍历j的过程中取最小的dp[i]！

可以有dp[j] + 1推出，当[j + 1, i] 为回文子串

dp数组如何初始化

首先来看一下dp[0]应该是多少。

dp[i]：范围是[0, i]的回文子串，最少分割次数是dp[i]。

那么dp[0]一定是0，长度为1的字符串最小分割次数就是0。这个是比较直观的。

在看一下非零下标的dp[i]应该初始化为多少？

在递推公式dp[i] = min(dp[i], dp[j] + 1) 中我们可以看出每次要取最小的dp[i]。

那么非零下标的dp[i]就应该初始化为一个最大数，这样递推公式在计算结果的时候才不会被初始值覆盖！

如果非零下标的dp[i]初始化为0，在那么在递推公式中，所有数值将都是零。

非零下标的dp[i]初始化为一个最大数。

代码如下：

vector<int> dp(s.size(), INT_MAX);
dp[0] = 0;

其实也可以这样初始化，更具dp[i]的定义，dp[i]的最大值其实就是i，也就是把每个字符分割出来。

所以初始化代码也可以为：

vector<int> dp(s.size());
for (int i = 0; i < s.size(); i++) dp[i] = i;

确定遍历顺序

根据递推公式：dp[i] = min(dp[i], dp[j] + 1);

j是在[0，i]之间，所以遍历i的for循环一定在外层，这里遍历j的for循环在内层才能通过计算过的dp[j]数值推导出dp[i]。

代码如下：

for (int i = 1; i < s.size(); i++) {
    if (isPalindromic[0][i]) { // 判断是不是回文子串
        dp[i] = 0;
        continue;
    }
    for (int j = 0; j < i; j++) {
        if (isPalindromic[j + 1][i]) {
            dp[i] = min(dp[i], dp[j] + 1);
        }
    }
}

大家会发现代码里有一个isPalindromic函数，这是一个二维数组isPalindromic[i][j]，记录[i, j]是不是回文子串。

那么这个isPalindromic[i][j]是怎么的代码的呢？

就是其实这两道题目的代码：

647. 回文子串
5.最长回文子串

所以先用一个二维数组来保存整个字符串的回文情况。

代码如下：

vector<vector<bool>> isPalindromic(s.size(), vector<bool>(s.size(), false));
for (int i = s.size() - 1; i >= 0; i--) {
    for (int j = i; j < s.size(); j++) {
        if (s[i] == s[j] && (j - i <= 1 || isPalindromic[i + 1][j - 1])) {
            isPalindromic[i][j] = true;
        }
    }
}

举例推导dp数组

以输入："aabc" 为例：

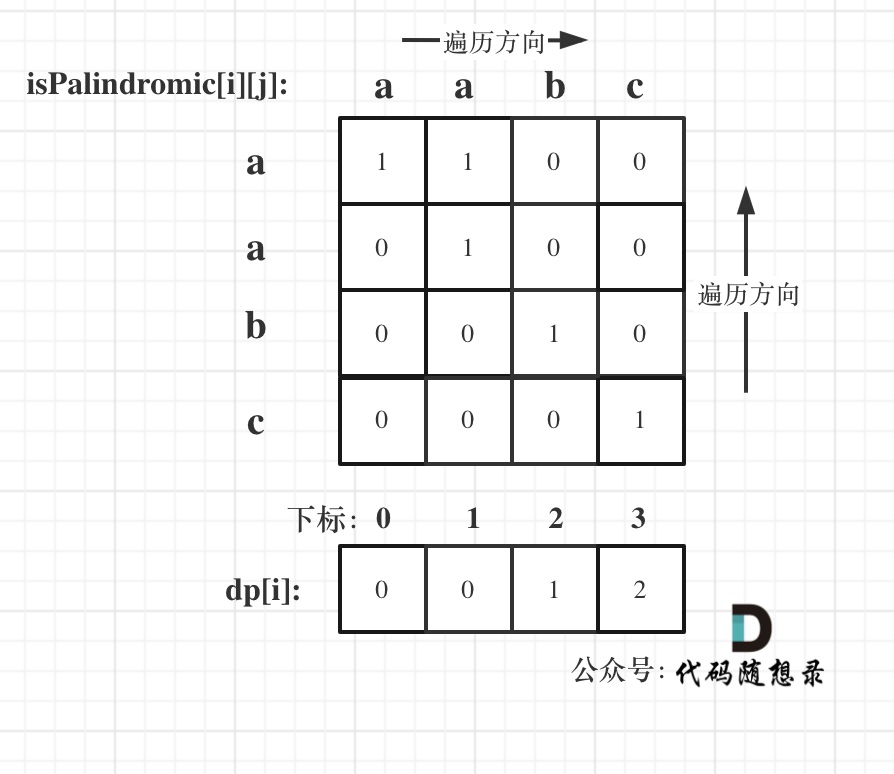
以上分析完毕，代码如下：

class Solution {
public:
    int minCut(string s) {
        vector<vector<bool>> isPalindromic(s.size(), vector<bool>(s.size(), false));
        for (int i = s.size() - 1; i >= 0; i--) {
            for (int j = i; j < s.size(); j++) {
                if (s[i] == s[j] && (j - i <= 1 || isPalindromic[i + 1][j - 1])) {
                    isPalindromic[i][j] = true;
                }
            }
        }
        // 初始化
        vector<int> dp(s.size(), 0);
        for (int i = 0; i < s.size(); i++) dp[i] = i;

        for (int i = 1; i < s.size(); i++) {
            if (isPalindromic[0][i]) {
                dp[i] = 0;
                continue;
            }
            for (int j = 0; j < i; j++) {
                if (isPalindromic[j + 1][i]) {
                    dp[i] = min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[s.size() - 1];

    }
};

其他语言版本

Java

class Solution {

    public int minCut(String s) {
        if(null == s || "".equals(s)){
            return 0;
        }
        int len = s.length();
        // 1.
        // 记录子串[i..j]是否是回文串
        boolean[][] isPalindromic = new boolean[len][len];
        // 从下到上，从左到右
        for(int i = len - 1; i >= 0; i--){
            for(int j = i; j < len; j++){
                if(s.charAt(i) == s.charAt(j)){
                    if(j - i <= 1){
                        isPalindromic[i][j] = true;
                    } else{
                        isPalindromic[i][j] = isPalindromic[i + 1][j - 1];
                    }
                } else{
                    isPalindromic[i][j] = false;
                }
            }
        }

        // 2.
        // dp[i] 表示[0..i]的最小分割次数
        int[] dp = new int[len];
        for(int i = 0; i < len; i++){
            //初始考虑最坏的情况。 1个字符分割0次， len个字符分割 len - 1次
            dp[i] = i;
        }

        for(int i = 1; i < len; i++){
            if(isPalindromic[0][i]){
                // s[0..i]是回文了，那 dp[i] = 0, 一次也不用分割
                dp[i] = 0;
                continue;
            }
            for(int j = 0; j < i; j++){
                // 按文中的思路，不清楚就拿 "ababa" 为例，先写出 isPalindromic 数组，再进行求解
                if(isPalindromic[j + 1][i]){
                    dp[i] = Math.min(dp[i], dp[j] + 1);
                }
            }
        }
        return dp[len - 1];
    }
}

Python

class Solution:
    def minCut(self, s: str) -> int:

        isPalindromic=[[False]*len(s) for _ in range(len(s))]

        for i in range(len(s)-1,-1,-1):
            for j in range(i,len(s)):
                if s[i]!=s[j]:
                    isPalindromic[i][j] = False
                elif  j-i<=1 or isPalindromic[i+1][j-1]:
                    isPalindromic[i][j] = True

        # print(isPalindromic)
        dp=[sys.maxsize]*len(s)
        dp[0]=0

        for i in range(1,len(s)):
            if isPalindromic[0][i]:
                dp[i]=0
                continue
            for j in range(0,i):
                if isPalindromic[j+1][i]==True:
                    dp[i]=min(dp[i], dp[j]+1)
        return dp[-1]

Go

func minCut(s string) int {
    isValid := make([][]bool, len(s))
    for i := 0; i < len(isValid); i++ {
        isValid[i] = make([]bool, len(s))
        isValid[i][i] = true
    }
    for i := len(s) - 1; i >= 0; i-- {
        for j := i + 1; j < len(s); j++ {
            if s[i] == s[j] && (isValid[i + 1][j - 1] || j - i == 1) {
                isValid[i][j] = true
            }
        }
    }

    dp := make([]int, len(s))
    for i := 0; i < len(s); i++ {
        dp[i] = math.MaxInt
    }
    for i := 0; i < len(s); i++ {
        if isValid[0][i] {
            dp[i] = 0
            continue
        }
        for j := 0; j < i; j++ {
            if isValid[j + 1][i] {
                dp[i] = min(dp[i], dp[j] + 1)
            }
        }
    }
    return dp[len(s) - 1]
}

func min(i, j int) int {
    if i < j {
        return i
    } else {
        return j
    }
}

JavaScript

var minCut = function(s) {
    const len = s.length;
    // 二维数组isPalindromic来保存整个字符串的回文情况
    const isPalindromic = new Array(len).fill(false).map(() => new Array(len).fill(false));
    for(let i = len - 1; i >= 0; i--){
        for(let j = i; j < len; j++){
            if(s[i] === s[j] && (j - i <= 1 || isPalindromic[i + 1][j - 1])){
                isPalindromic[i][j] = true;
            }
        }
    }
    // dp[i]：范围是[0, i]的回文子串，最少分割次数是dp[i]
    const dp = new Array(len).fill(0);
    for(let i = 0; i < len; i++) dp[i] = i; // 初始化 dp[i]的最大值其实就是i，也就是把每个字符分割出来
    for(let i = 1; i < len; i++){
        if(isPalindromic[0][i]){ // 判断是不是回文子串
            dp[i] = 0;
            continue;
        }
        /* 
        如果要对长度为[0, i]的子串进行分割，分割点为j。
        那么如果分割后，区间[j + 1, i]是回文子串，那么dp[i] 就等于 dp[j] + 1。
        这里可能有同学就不明白了，为什么只看[j + 1, i]区间，不看[0, j]区间是不是回文子串呢？
        那么在回顾一下dp[i]的定义： 范围是[0, i]的回文子串，最少分割次数是dp[i]。
        [0, j]区间的最小切割数量，我们已经知道了就是dp[j]。
        此时就找到了递推关系，当切割点j在[0, i] 之间时候，dp[i] = dp[j] + 1;
        本题是要找到最少分割次数，所以遍历j的时候要取最小的dp[i]。dp[i] = Math.min(dp[i], dp[j] + 1);
         */
        for(let j = 0; j < i; j++){
            if(isPalindromic[j + 1][i]){
                dp[i] = Math.min(dp[i], dp[j] + 1);
            }
        }
    }
    return dp[len - 1];
};

0132.分割回文串II

132. 分割回文串 II

思路

其他语言版本

Java

Python

Go

JavaScript