61、数据结构与算法Python：图的应用（词梯问题）

词梯Word Ladder问题

由 “ 爱 丽 丝 漫 游 奇 境 ” 的 作 者 Lewis

Carroll在1878年所发明的单词游戏

从一个单词演变到另一个单词， 其中的过程可以经过多个中间单词

要求是相邻两个单词之间差异只能是1个字母，如FOOL变SAGE：
FOOL >> POOL >> POLL >> POLE >> PALE>> SALE >> SAGE

我们的目标是找到最短的单词变换序列

采用图来解决这个问题的步骤如下：

将可能的单词之间的演变关系表达为图，采用“广度优先搜索 BFS”，来搜寻从开始单词到结束单词之间的所有有效路径，选择其中最快到达目标单词的路径

词梯问题：构建单词关系图

首先是如何将大量的单词集放到图中

将单词作为顶点的标识Key，如果两个单词之间仅相差1个字母，就在它们之间设一条边

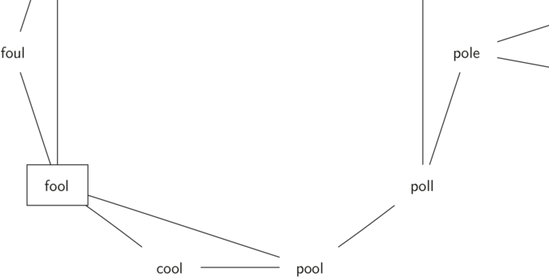
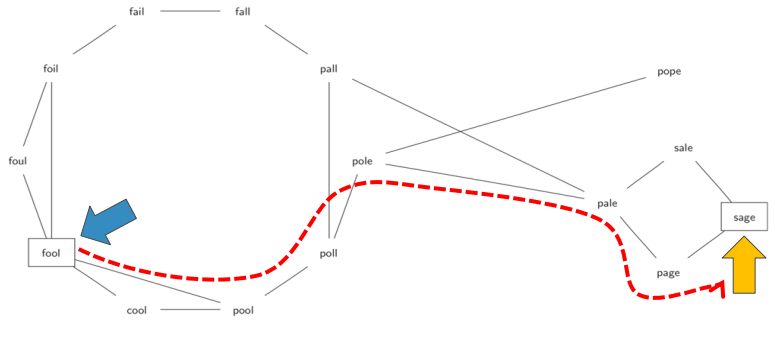
下图是从FOOL到SAGE的词梯解， 所用的图是无向图， 边没有权重

FOOL到SAGE的每条路径都是一个解

单词关系图可以通过不同的算法来构建（以4个字母的单词表为例）

首先是将所有单词作为顶点加入图中，再设法建立顶点之间的边

建立边的最直接算法， 是对每个顶点（单词） ， 与其它所有单词进行比较， 如果相差仅1个字母， 则建立一条边

时间复杂度是O(n^2)，对于所有4个字母的5110个单词，需要超过2600万次比较

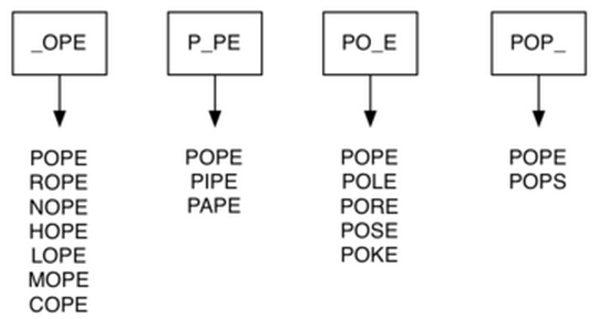
改进的算法是创建大量的桶， 每个桶可以存放若干单词

桶标记是去掉1个字母，通配符“_”占空的单词

所有匹配标记的单词都放到这个桶里

所有单词就位后，再在同一个桶的单词之间建立边即可

词梯问题： 采用字典建立桶

def buildGraph(wordFile):
    d = {
   
     }
    g = Grapgh()
    wfile = open(wordFile, 'r')
    for line in wfile:
        word = line[:-1]
        for i in range(len(word)):
            bucket = word[:i] + '_' + word[i+1:]
            if bucket in d:
                # 4字母单词可属于4个桶
                d[bucket].append(word)
            else:
                d[bucket] = [word]
    for bucket in d.keys():
        # 同一个桶单词之间建立边
        for word1 in d[bucket]:
            for word2 in d[bucket]:
                if word1 != word2:
                    g.addEdge(word1, word2)
    return g

词梯问题：构建单词关系图

样例数据文件包含了5,110个4字母单词

可从课程网站下载

如果采用邻接矩阵表示这个单词关系图，则需要2,600万个矩阵单元

5,110*5,110= 26,112,100，而单词关系图总计有53,286条边，仅仅达到矩阵单元数量的0.2%

单词关系图是一个非常稀疏的图

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: