43、数据结构与算法Python：映射抽象数据类型及Python实现-程序员快看-教程，程序员编程资料站

抽象数据类型“映射”:ADT Map

Python最有用的数据类型之一“字典”

字典是一种可以保存key-data键值对的数据类型

其中关键码key可用于查询关联的数据值data

这种键值关联的方法称为“映射Map”

ADT Map的结构是键-值关联的无序集合

关键码具有唯一性，通过关键码可以唯一确定一个数据值

ADT Map定义的操作如下：

Map()：创建一个空映射，返回空映射对象；
put(key, val)：将key-val关联对加入映射中，如果key已存在，将val替换旧关联值；
get(key)：给定key，返回关联的数据值，如不存在，则返回None；
del：通过del map[key]的语句形式删除key-val关联；
len()：返回映射中key-val关联的数目；
in：通过key in map的语句形式，返回key是否存在于关联中，布尔值

实现ADT Map

使用字典的优势在于，给定关键码key，能够很快得到关联的数据值data

为了达到快速查找的目标，需要一个支持高效查找的ADT实现

可以采用列表数据结构加顺序查找或者二分查找，当然，更为合适的是使用前述的散列表来实现，这样查找可以达到最快O(1)的性能

下面，我们用一个HashTable类来实现ADT Map，该类包含了两个列表作为成员

其中一个slot列表用于保存key
另一个平行的data列表用于保存数据项

在slot列表查找到一个key的位置以后，在data列表对应相同位置的数据项即为关联数据

实现ADT Map：应用实例

保存key的列表就作为散列表来处理，这样可以迅速查找到指定的key

注意散列表的大小，虽然可以是任意数，但考虑到要让冲突解决算法能有效工作，应该选择为素数。

class HashTable:
    def __init__(self):
        self.size = 11
        self.slots = [None] * self.size
        self.data = [None] * self.size

实现ADT Map： put方法代码

hashfunction方法采用了简单求余方法来实现散列函数，而冲突解决则采用线性探测“加1”再散列函数。

def hashfunction(self, key):
    return key % self.size

def rehash(self, oldhash):
    return (oldhash + 1) % self.size

def put(self, key, data):
    hashvalue = self.hashfunction(key)

    if self.slots[hashvalue] == None:
        # key不存在，未冲突
        self.slots[hashvalue] = key
        self.data[hashvalue] = data
    else:
        # key已存在，替换val
        if self.slots[hashvalue] == key:
            self.data[hashvalue] = data
        else:
            nextslot = self.rehash(hashvalue)
            # 散列冲突，再散列，直到找到空槽或者key
            while self.slots[nextslot] != None and self.slots[nextslot] != key:
                nextslot = self.rehash(nextslot)

            if self.slots[nextslot] == None:
                self.slots[nextslot] = key
                self.data[nextslot] = data
            else:
                self.data[nextslot] = data

实现ADT Map： get方法

def get(self, key):
    # 标记散列值为查找起点
    startslot = self.hashfunction(key)

    data = None
    stop = False
    found = False
    position = startslot
    # 找key，直到空槽或回到起点
    while self.slots[position] != None and not found and not stop:
        if self.slots[position] == key:
            found = True
            data = self.data[position]
        else:
            # 未找到key，再散列继续找
            position=self.rehash(position)
            if position == startslot:
                # 回到起点
                stop = True
    return data

实现ADT Map：附加代码

通过特殊方法实现[]访问

def __getitem__(self, key):
    return self.get(key)

def __setitem__(self, key, data):
    self.put(key, data)

散列算法分析

散列在最好的情况下，可以提供O(1)常数级时间复杂度的查找性能

由于散列冲突的存在，查找比较次数就没有这么简单

评估散列冲突的最重要信息就是负载因子*，一般来说：

如果*较小，散列冲突的几率就小，数据项通常会保存在其所属的散列槽中
如果*较大，意味着散列表填充较满，冲突会越来越多，冲突解决也越复杂，也就需要更多的比较来找到空槽；如果采用数据链的话，意味着每条链上的数据项增多

如果采用线性探测的开放定址法来解决冲突（*在0~1之间）

成功的查找，平均需要比对次数为：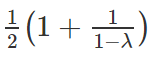
不成功的查找，平均比对次数为：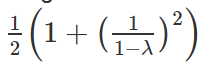

如果采用数据链来解决冲突（*可大于1）

成功的查找，平均需要比对次数为： 1+*/2
不成功的查找，平均比对次数为： *

43、数据结构与算法Python：映射抽象数据类型及Python实现