53、数据结构与算法Python：二叉查找树及操作

二叉查找树Binary Search Tree

在ADT Map的实现方案中， 可以采用不同的数据结构和搜索算法来保存和查找Key， 前面已经实现了两个方案

有序表数据结构+二分搜索算法，散列表数据结构+散列及冲突解决算法

下面我们来试试用二叉查找树保存key，实现key的快速搜索

在ADT Map的实现方案中， 可以采用不同的数据结构和搜索算法来保存和查找Key， 前面已经实现了两个方案

有序表数据结构+二分搜索算法，散列表数据结构+散列及冲突解决算法

下面我们来试试用二叉查找树保存key，实现key的快速搜索

二叉查找树： ADT Map

复习一下ADT Map的操作：

• Map()：创建一个空映射
• put(key, val)：将key-val关联对加入映射中，如果key已经存在，则将val替换旧关联值；
• get(key)：给定key，返回关联的数据值，如不存在，则返回None；
• del：通过del map[key]的语句形式删除keyval关联；
• len()：返回映射中key-val关联的数目；
• in：通过key in map的语句形式，返回key是否存在于关联中，布尔值

二叉查找树BST的性质

比父节点小的key都出现在左子树， 比父节点大的key都出现在右子树。

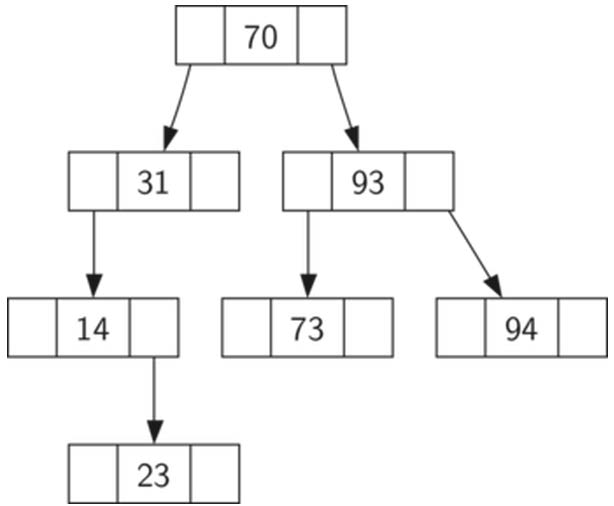
按照70,31,93,94,14,23,73的顺序插入

首先插入的70成为树根

31比70小，放到左子节点
93比70大，放到右子节点
94比93大，放到右子节点
14比31小，放到左子节点
23比14大，放到其右
73比93小，放到其左

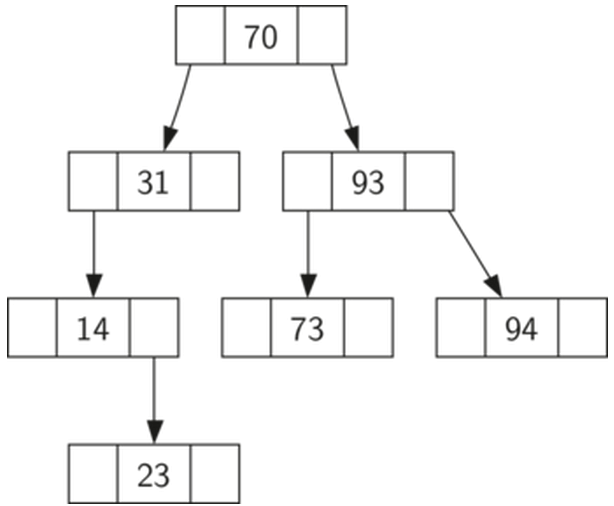
注意：插入顺序不同， 生成的BST也不同

二叉搜索树的实现：节点和链接结构

需要用到BST和TreeNode两个类， BST的root成员引用根节点TreeNode

class BinarySearchTree:
    def __init__(self):
        self.root = None
        self.size = 0

    def length(self):
        return self.size

    def __len__(self):
        return self.size

    def __iter__(self):
        return self.root.__iter__()

二叉搜索树的实现： TreeNode类

class TreeNode:
    def __init__(self, key, val, left=None, right=None, parent=None):
        # 键值
        self.key = key
        # 数据项
        self.payload = val
        # 左右子节点
        self.leftChild = left
        self.rightChild = right
        # 父节点
        self.parent = parent

    def hasLeftChild(self):
        return self.leftChild

    def hasRightChild(self):
        return self.rightChild

    def isLeftChild(self):
        return self.parent and self.parent.leftChild == self

    def isRightChild(self):
        return self.parent and self.parent.rightChild == self
    
    def isRoot(self):
        return not self.parent
    
    def isLeaf(self):
        return not (self.rightChild or self.leftChild)
    
    def hasAnyChildren(self):
        return self.rightChild or self.leftChild
    
    def hasBothChildren(self):
        return self.rightChild and self.leftChild
    
    def replaceNodeData(self, key, value, lc, rc):
        self.key = key
        self.payload = value
        self.leftChild = lc
        self.rightChild = rc
        if self.hasLeftChild():
            self.leftChild.parent = self
        if self.hasRightChild():
            self.rightChild.parent = self

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: