什么是递归Recursion?
递归是一种解决问题的方法, 其精髓在于
将问题分解为规模更小的相同问题,持续分解,直到问题规模小到可以用非常简单直接的方式来解决。递归的问题分解方式非常独特,其算法方面的明显特征就是:在算法流程中调用自身。
递归为我们提供了一种对复杂问题的优雅解决方案, 精妙的递归算法常会出奇简单, 令人赞叹。
初识递归:数列求和
问题:给定一个列表, 返回所有数的和
列表中数的个数不定,需要一个循环和一个累加变量来迭代求和
程序很简单, 但假如没有循环语句?
既不能用 for,也不能用 while 还能对不确定长度的列表求和么?
def listsum(numList):
theSum = 0
for i in numList:
theSum = theSum + i
return theSum
print(listsum([1, 3, 5, 7, 9]))
我们认识到求和实际上最终是由一次次的加法实现的, 而加法恰有2个操作数, 这个是确定的。
看看怎么想办法, 将问题规模较大的列表求和, 分解为规模较小而且固定的2个数求和(加法) ?
同样是求和问题,但规模发生了变化,符合递归解决问题的特征!
换个方式来表达数列求和:全括号表达式
(1+(3+(5+(7+9))))
上面这个式子, 最内层的括号(7+9), 这是无需循环即可计算的, 实际上整个求和的过程是这样:
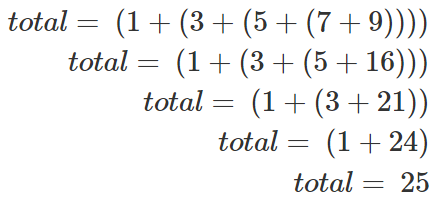
观察上述过程中所包含的重复模式, 可以把求和问题归纳成这样:
数列的和=“首个数”+“余下数列”的和
如果数列包含的数少到只有1个的话, 它的和就是这个数了
这是规模小到可以做最简单的处理

上面的递归算法变成程序
def listsum(numList):
if len(numList) == 1:
return numList[0]
else:
return numList[0] + listsum(numList[1:])
print(listsum([1, 3, 5, 7, 9]))
上面程序的要点:
1、 问题分解为更小规模的相同问题,并表现为“调用自身”;
2、 对“最小规模”问题的解决:简单直接;
递归程序如何被执行?
递归函数调用和返回过程的链条
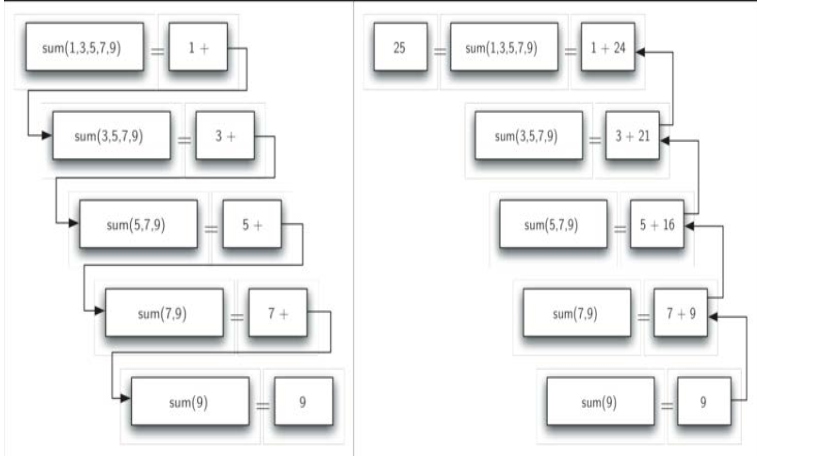
递归“三定律”
为了向阿西莫夫的“机器人三定律”致敬, 递归算法也总结出“三定律”
1、 递归算法必须有一个基本结束条件(最小规;
模问题的直接解决)
2、 递归算法必须能改变状态向基本结束条件演;
进(减小问题规模)
3、 递归算法必须调用自身(解决减小了规模的;
相同问题)
递归“三定律”:数列求和问题
1、 数列求和问题首先具备了基本结束条件:当列表长度为1的时候,直接输出所包含的唯一数;
2、 数列求和处理的数据对象是一个列表,而基本结束条件是长度为1的列表,那递归算法就要改变列表并向长度为1的状态演进我们看到其具体做法是将列表长度减少1;
3、 调用自身是递归算法中最难理解的部分,实际上我们理解为“问题分解成了规模更小的相同问题”就可以了在数列求和算法中就是“更短数列的求和问题”;
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: