36、数据结构与算法Python：归并排序算法及分析

归并排序Merge Sort

下面我们来看看分治策略在排序中的应用

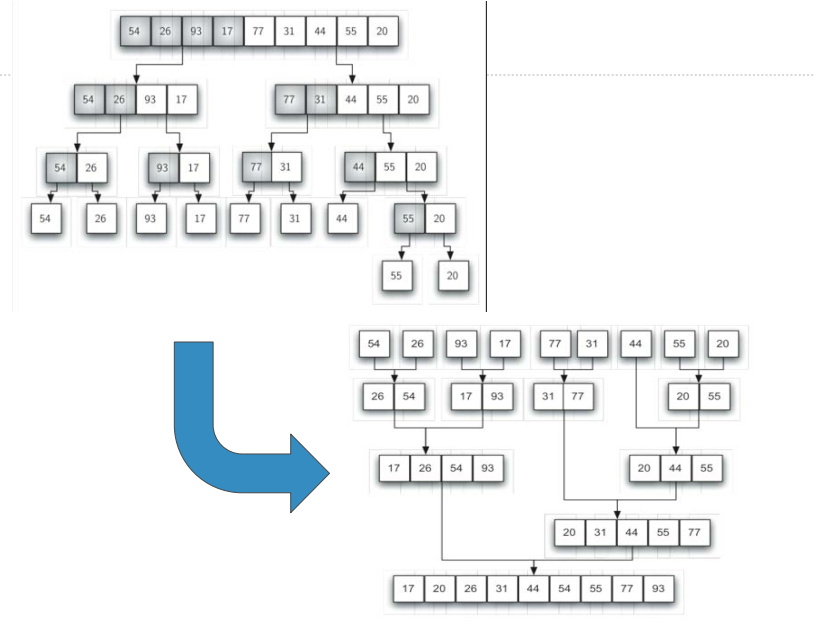
归并排序是递归算法， 思路是将数据表持续分裂为两半， 对两半分别进行归并排序

递归的基本结束条件是：数据表仅有1个数据项，自然是排好序的；
缩小规模：将数据表分裂为相等的两半，规模减为原来的二分之一；
调用自身：将两半分别调用自身排序，然后将分别排好序的两半进行归并，得到排好序的数据表

代码一：

def mergeSort(alist):
    if len(alist) > 1:
        mid = len(alist) // 2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        mergeSort(lefthalf)
        mergeSort(righthalf)

        i = j = k = 0
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k] = lefthalf[i]
                i = i + 1
            else:
                # 拉链式交错把左右半部从小到大归并到结果列表中
                alist[k] = righthalf[j]
                j = j + 1
            k = k + 1
        while i < len(lefthalf):
            # 归并左半部剩余项
            alist[k] = lefthalf[i]
            i = i + 1
            k = k + 1

        while j < len(righthalf):
            alist[k] = righthalf[j]
            j = j + 1
            k = k + 1
alist = [11, 21, 1, 23, 14, 2, 5, 77]
mergeSort(alist)
print(alist)

另一个归并排序代码（更Pythonic）

def merge_sort(lst):
    # 递归结束条件
    if len(lst) <= 1:
        return lst

    # 分解问题，并递归调用
    middle = len(lst) // 2
    left = merge_sort(lst[:middle]) # 左半部排好序
    right = merge_sort(lst[middle:]) # 右半部排好序

    # 合并左右半部，完成排序
    merged = []
    while left and right:
        if left[0] <= right[0]:
            merged.append(left.pop(0))
        else:
            merged.append(right.pop(0))

    merged.extend(right if right else left)
    return merged

归并排序：算法分析

将归并排序分为两个过程来分析： 分裂和归并

分裂的过程， 借鉴二分查找中的分析结果， 是对数复杂度， 时间复杂度为O(log n)

归并的过程， 相对于分裂的每个部分， 其所有数据项都会被比较和放置一次， 所以是线性复杂度， 其时间复杂度是O(n)

综合考虑，每次分裂的部分都进行一次O(n)的数据项归并，总的时间复杂度是O(nlog n)

最后， 我们还是注意到两个切片操作

为了时间复杂度分析精确起见，可以通过取消切片操作，改为传递两个分裂部分的起始点和终止点，也是没问题的，只是算法可读性稍微牺牲一点点。

我们注意到归并排序算法使用了额外1倍的存储空间用于归并

这个特性在对特大数据集进行排序的时候要考虑进去

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: