08、数据结构与算法Python：栈的应用（十进制转换为二进制）

所谓的“进制”， 就是用多少个字符来表示整数

十进制是0～9这十个数字字符，二进制是0、 1两个字符

十进制转换为二进制， 采用的是“除以2求余数”的算法

将整数不断除以2，每次得到的余数就是由低到高的二进制位

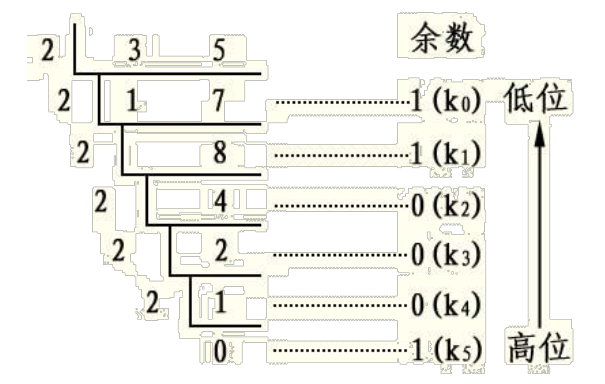
“除以2”的过程， 得到的余数是从低到高的次序， 而输出则是从高到低， 所以需要一个栈来反转次序

def divideBy2(decNumber):
    remstack = Stack()

    while decNumber > 0:
        rem = decNumber % 2
        remstack.push(rem)
        decNumber = decNumber // 2

    binString = ""
    while not remstack.isEmpty():
        binString = binString + str(remstack.pop())

    return binString

print(divideBy2(42))

扩展到更多进制转换

十进制转换为二进制的算法， 很容易可以扩展为转换到任意N进制

只需要将“除以2求余数”算法改为“除以N求余数”算法就可以

主要的问题是如何表示八进制及十六进制

二进制有两个不同数字0、 1
十进制有十个不同数字0、 1、 2、 3、 4、 5、 6、7、 8、 9
八进制可用八个不同数字0、 1、 2、 3、 4、 5、 6、 7
十六进制的十六个不同数字则是0、 1、 2、 3、 4、 5、 6、 7、 8、 9、 A、 B、 C、 D、 E、 F

十进制转换为十六以下任意进制：代码

def baseConverter(decNumber, base):
    digits = "0123456789ABCDEF"

    remstack = Stack()

    while decNumber > 0:
        rem = decNumber % base
        remstack.push(rem)
        decNumber = decNumber // base

    newString = ""
    while not remstack.isEmpty():
        newString = newString + digits[remstack.pop()]

    return newString

print(baseConverter(25, 2))
print(baseConverter(3000, 16))

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: