优先队列Priority Queue
前面我们学习了一种FIFO数据结构队列
队列有一种变体称为“优先队列”。
银行窗口取号排队, VIP客户可以插到队首,操作系统中执行关键任务的进程或用户特别指定,进程在调度队列中靠前
优先队列的出队跟队列一样从队首出队;
但在优先队列内部, 数据项的次序却是由“优先级”来确定:
高优先级的数据项排在队首,而低优先级的数据项则排在后面。这样,优先队列的入队操作就比较复杂,需要将数据项根据其优先级尽量挤到队列前方。
思考:有什么方案可以用来实现优先队列?
出队和入队的复杂度大概是多少?
二叉堆Binary Heap实现优先队列
实现优先队列的经典方案是采用二叉堆数据结构
二叉堆能够将优先队列的入队和出队复杂度都保持在O(log n)
二叉堆的有趣之处在于, 其逻辑结构上象二叉树, 却是用非嵌套的列表来实现的!
最小key排在队首的称为“最小堆min heap”
反之,最大key排在队首的是“最大堆max heap”
ADT BinaryHeap的操作定义如下:
- BinaryHeap():创建一个空二叉堆对象;
- insert(k):将新key加入到堆中;
- findMin():返回堆中的最小项,最小项仍保留在堆中;
- delMin():返回堆中的最小项,同时从堆中删除;
- isEmpty():返回堆是否为空;
- size():返回堆中key的个数;
- buildHeap(list):从一个key列表创建新堆
ADT BinaryHeap的操作示例
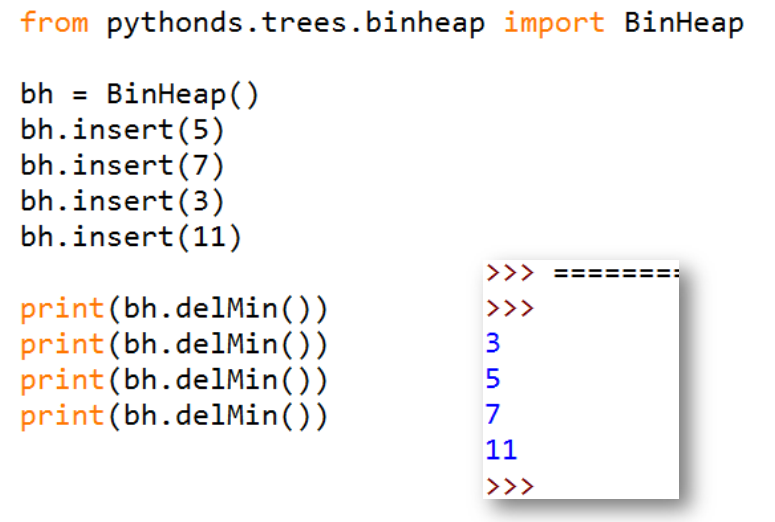
用非嵌套列表实现二叉堆
为了使堆操作能保持在对数水平上, 就必须采用二叉树结构;
同样, 如果要使操作始终保持在对数数量级上, 就必须始终保持二叉树的“平衡”
树根左右子树拥有相同数量的节点
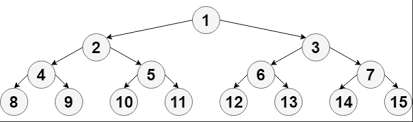
我们采用“完全二叉树”的结构来近似实现“平衡”
完全二叉树,叶节点最多只出现在最底层和次底层,而且最底层的叶节点都连续集中在最左边,每个内部节点都有两个子节点, 最多可有1个节点例外
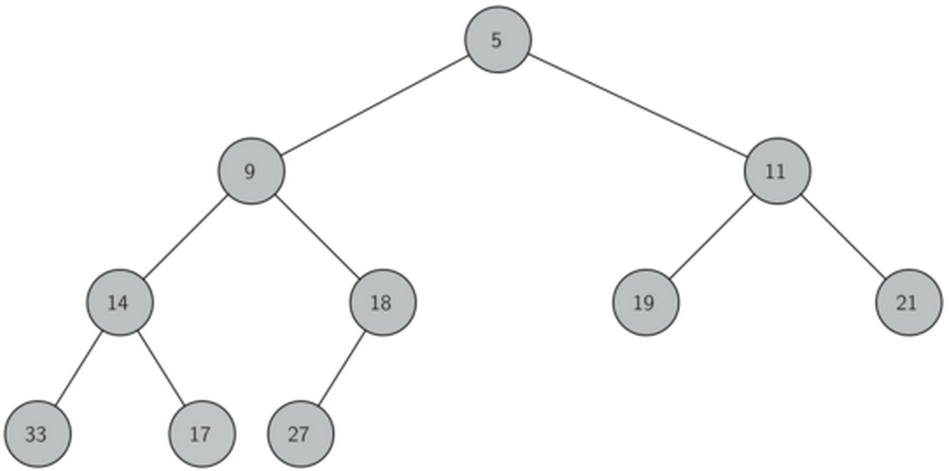
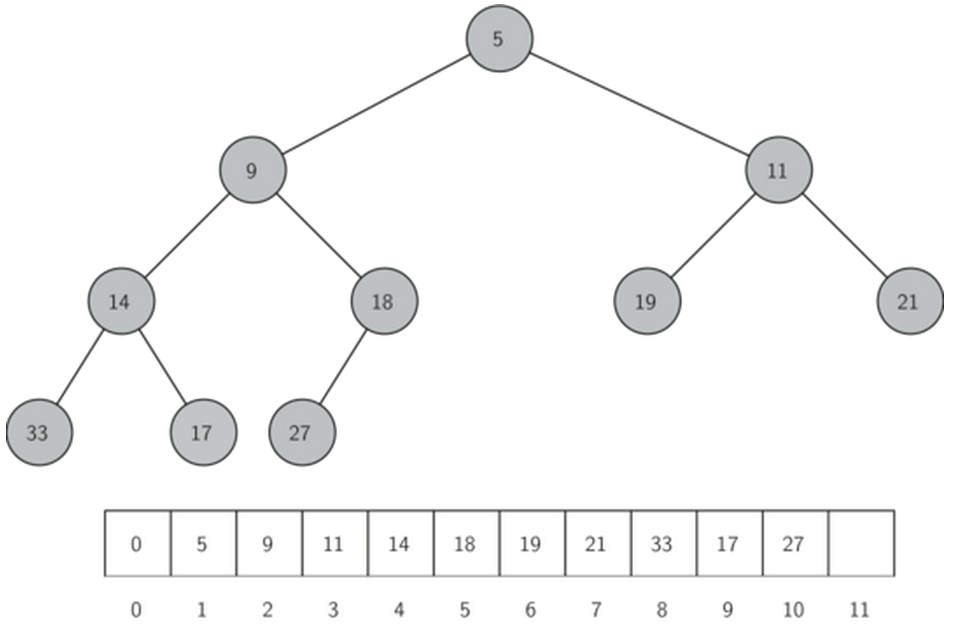
完全二叉树的列表实现及性质
完全二叉树由于其特殊性, 可以用非嵌套列表, 以简单的方式实现, 具有很好性质
如果节点的下标为p,那么其左子节点下标为2p,右子节点为2p+1,其父节点下标为p//2
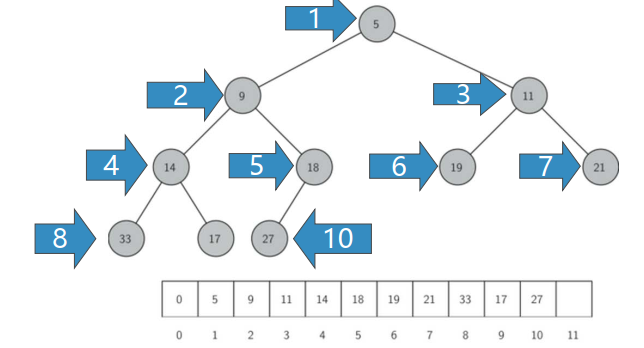
堆次序Heap Order
任何一个节点x, 其父节点p中的key均小于x中的key
这样,符合“堆”性质的二叉树,其中任何一条路径,均是一个已排序数列, 根节点的key最小
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: