整数转换为任意进制
我们用最熟悉的十进制分析下这个问题
十进制有十个不同符号: convString ="0123456789"比十小的整数,转换成十进制, 直接查表就可以了: convString[n]想办法把比十大的整数,拆成一系列比十小的整数,逐个查表比如七百六十九,拆成七、六、九,查表得到769就可以了
所以, 在递归三定律里, 我们找到了“基本结束条件”, 就是小于十的整数
拆解整数的过程就是向“基本结束条件”演进的过程
我们用整数除, 和求余数两个计算来将整数一步步拆开
除以“进制基base”(// base)对“进制基”求余数(% base)
问题就分解为:
余数总小于“进制基base”,是“基本结束条件”,可直接进行查表转换整数商成为“更小规模”问题,通过递归调用自身解决
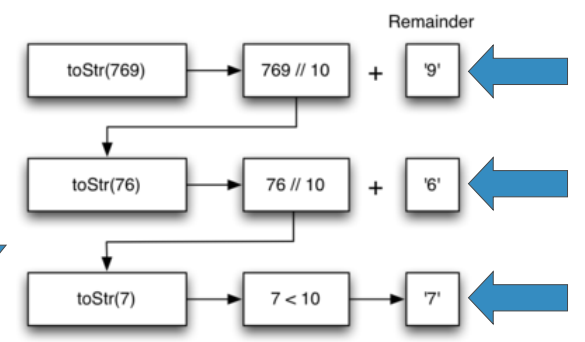
下面就是递归算法的代码
def toStr(n, base):
convertString = "0123456789ABCDEF"
if n < base:
return convertString[n]
else:
return toStr(n//base, base) + convertString[n % base]
print(toStr(1453, 16))
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: