03、数据结构与算法Python：变位词判断问题-程序员快看-教程，程序员编程资料站

”变位词“判断问题

问题描述

所谓”变位词“是指两个词之间存在组成字母的重新排列关系，如：heart 和 earth，python 和 typhon，为了简单起见，假设参与判断的两个词仅由小写字母构成，而且长度相等

解题目标：写一个bool函数，以两个词作为参数，返回这两个词是否变位词

可以很好的展示同一问题的不同数量级算法

解法一：逐字检查

解法思路

将词1中的字符逐个到词2中检查是否存在存在就”打勾“标记（防止重复检查），如果每个字符都能找到，则两个词是变位词只要有1个字符找不到，就不是变位词

def anagramSolution1(s1, s2):
    alist = list(s2) # 复制s2到列表
    pos1 = 0
    stillOK = True
    while pos1 < len(s1) and stillOK: # 循环s1的每个字符
        pos2 = 0
        found = False
        while pos2 < len(alist) and not found:
            if s1[pos1] == alist[pos2]: # 在s2逐个对比
                found = True
            else:
                pos2 = pos2 + 1
        if found:
            alist[pos2] = None # 找到，打勾
        else:
            stillOK = False # 未找到，失败
        pos1 = pos1 + 1
    return stillOK

print(anagramSolution1("abcd", "dcba"))

数量级为O(n^2)

解法二：排序比较

解法思路

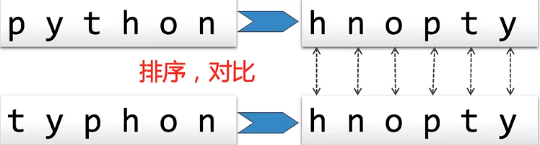
将两个字符串都按照字母顺序排好序，在逐个字符对比是否相同，如果相同则是变位词，有任何不同就不是变位词

def anagramSolution2(s1, s2):
    # 转为列表
    alist1 = list(s1)
    alist2 = list(s2)
    
    # 分别排序
    alist1.sort()
    alist2.sort()
    pos = 0
    matches = True
    while pos < len(s1) and matches:
        # 逐个对比
        if alist1[pos] == alist2[pos]:
            pos = pos + 1
        else:
            matches = False
    return matches

print(anagramSolution2("abcd", "dcba"))

1、粗看上去，本算法只有一个循环，最多执行n次，数量级是O(n)，但循环前面的两个sort并不是无代价的，如果查询下后面的章节，会发现排序算法采用不同的解决方案，其运行时间数量级差不多是O(n^2)或者O(nlogn)，大过循环的O(n)；
2、所以本算法时间主导的步骤是排序步骤；
3、本算法的运行时间数量级就等于排序过程的数量级O(nlogn)；

解法3：计数比较

解题思路：对比两个词种每个字母出现的次数，如果26个字母出现的次数都相同的话，这两个字符串就一定是变位词

具体做法：为每个词设置一个26位的计数器，先检查每个词，在计数器种设定好每个字母出现的次数

计算完成后，进入比较阶段，看两个字符串的计数器是否相同，如果相同则输出是变位词的结论

def anagramSolution3(s1, s2):
    c1 = [0] * 26
    c2 = [0] * 26
    # 分别都计数
    for i in range(len(s1)):
        pos = ord(s1[i]) - ord('a')
        c1[pos] = c1[pos] + 1
    for i in range(len(s2)):
        pos = ord(s2[i]) - ord('a')
        c2[pos] = c2[pos] + 1
    j = 0
    stillOK = True
    # 计数器比较
    while j < 26 and stillOK:
        if c1[j] == c2[j]:
            j = j + 1
        else:
            stillOK = False
    return stillOK

print(anagramSolution3("abcd", "dcba"))

1、计数比较算法中有3个循环迭代，但不象解法1那样存在嵌套循环，前两个循环用于对字符串进行计数，操作次数等于字符串长度n；
2、第3个循环用于计数器比较，操作次数总是26次；
3、所以总操作次数T(n)=2n+36，其数量级为O(n)，这是一个线性数量级的算法，是4个变位词判断算法种性能最优的；
4、值得注意的是，本算法依赖于两个长度为26的计数器列表，来保存字符计数，这相比前3个算法需要更多的存储空间，如果考虑由大字符集构成的词，还会需要更多存储空间；
5、牺牲存储空间来换取运行时间，或者相反，这种在时间空间之间的取舍和权衡，在选择问题解法的过程中经常会出现；