找零兑换问题:递归解法
我们来找一种肯定能找到最优解的方法
贪心策略是否有效依赖于具体的硬币体系
首先是确定基本结束条件, 兑换硬币这个问题最简单直接的情况就是, 需要兑换的找零, 其面值正好等于某种硬币
如找零25分,答案就是1个硬币!

其次是减小问题的规模, 我们要对每种硬币尝试1次, 例如美元硬币体系:
找零减去1分(penny)后,求兑换硬币最少数量(递归调用自身);
找零减去5分(nikel)后,求兑换硬币最少数量
找零减去10分(dime)后,求兑换硬币最少数量
找零减去25分(quarter)后,求兑换硬币最少数量
上述4项中选择最小的一个。
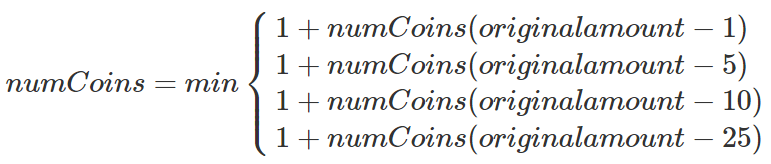
找零兑换问题:递归解法代码
def recMC(coinValueList, change):
minCoins = change
if change in coinValueList:
return 1
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMC(coinValueList, change-i)
if numCoins < minCoins:
minCoins = numCoins
return minCoins
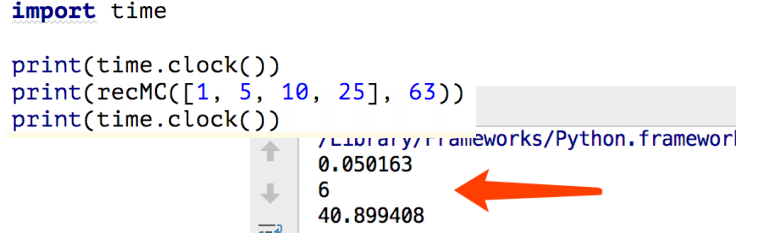
print(recMC([1, 5, 10, 25], 63))
递归解法虽然能解决问题, 但其最大的问题是: 极! 其! 低! 效!
对63分的兑换硬币问题,需要进行67,716,925次递归调用!在我这台笔记本电脑上花费了40秒时间得到解:6个硬币
找零兑换问题:递归解法分析
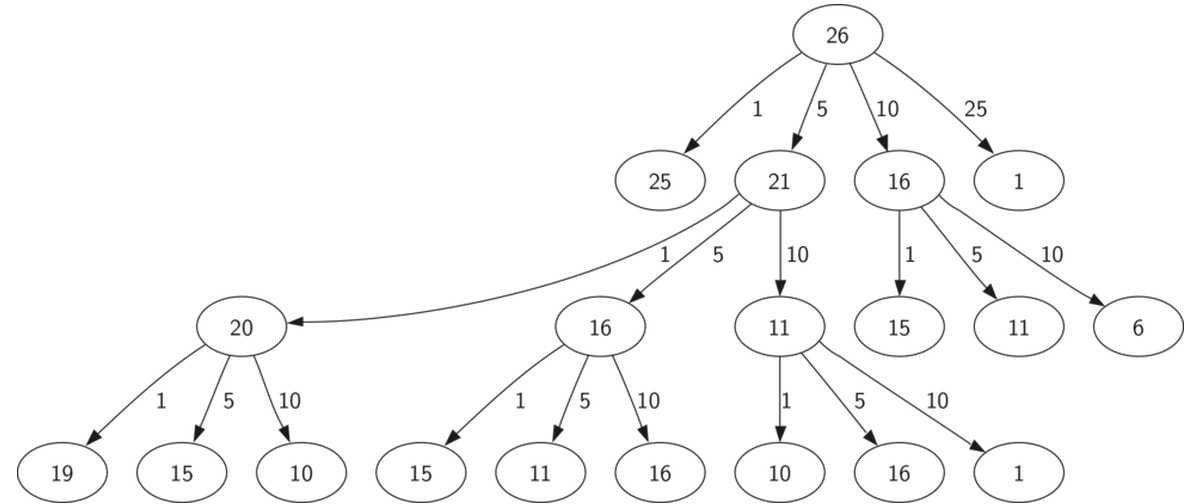
以26分兑换硬币为例, 看看递归调用过程(377次递归的一小部分)
我们发现一个重大秘密,就是重复计算太多!例如找零15分的,出现了3次!而它最终解决还要52次递归调用很明显,这个算法致命缺点是重复计算
找零兑换问题:递归解法改进
对这个递归解法进行改进的关键就在于消除重复计算
我们可以用一个表将计算过的中间结果保存起来,在计算之前查表看看是否已经计算过
这个算法的中间结果就是部分找零的最优解, 在递归调用过程中已经得到的最优解被记录下来
在递归调用之前,先查找表中是否已有部分找零的最优解如果有, 直接返回最优解而不进行递归调用,如果没有,才进行递归调用
找零兑换问题:递归解法改进代码
def recMC(coinValueList, change, knownResults):
minCoins = change
# 递归基本结束条件
if change in coinValueList:
# 记录最优解
knownResults[change] = 1
return 1
elif knownResults[change] > 0:
# 查表成功,直接用最优解
return knownResults[change]
else:
for i in [c for c in coinValueList if c <= change]:
numCoins = 1 + recMC(coinValueList, change-i, knownResults)
if numCoins < minCoins:
minCoins = numCoins
# 找到最优解,记录到表中
knownResults[change] = minCoins
return minCoins
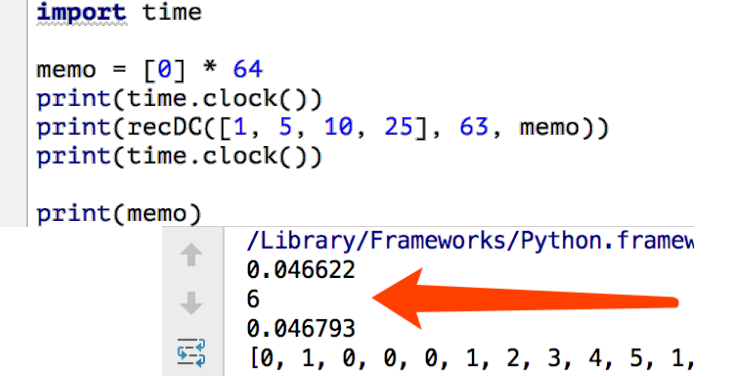
print(recMC([1, 5, 10, 25], 63, [0]*64))
改进后的解法, 极大减少了递归调用次数
对63分兑换硬币问题,仅仅需要221次递归调用是改进前的三十万分之一,瞬间返回!
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: