本章小结
在无序表或者有序表上的顺序查找, 其时间复杂度为O(n)
在有序表上进行二分查找, 其最差复杂度为O(log n)
散列表可以实现常数级时间的查找
完美散列函数作为数据一致性校验, 应用很广
区块链技术是一种去中心化的分布式数据库, 通过“工作量证明”机制来维持运行
冒泡、 选择和插入排序是O(n2)的算法
谢尔排序在插入排序的基础上进行了改进, 采用对递增子表排序的方法, 其时间复杂度可以在O(n)和O(n2)之间
归并排序的时间复杂度是O(nlog n), 但归并的过程需要额外存储空间
快速排序最好的时间复杂度是O(nlog n), 也不需要额外的存储空间, 但如果分裂点偏离列表中心的话, 最坏情况下会退化到O(n2)
算法的选择:一封同学来信
冒泡排序算法中提到一个对其改进的算法
利用“如果一趟比对未产生任何交换,则已排好序”的“短路”特性,消除无效比对,理应更快
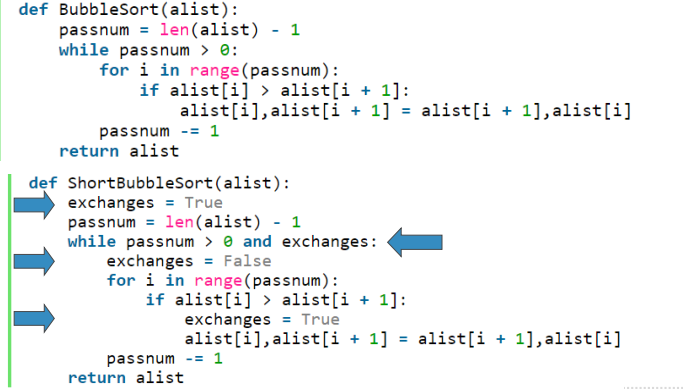
但有细心的同学自己动手做了试验, 结果不太乐观:
我试了一下排序算法
发现shortBubbleSort比BubbleSort慢很多啊
(每组数据运行10次取平均)
算法就是照着幻灯片上写的,为什么呢?

为什么理论和实际相差甚远?
到底还能不能愉快地选择一个好算法了?
ShortBubbleSort的“短路”优势高度依赖于数据的初始布局
如果数据布局的随机度很高,造成每趟比对都会发生交换的话, ShortBubbleSort就完全没有优势,还要额外付出一个exchanges变量和相应赋值语句的代价,反倒比原始的冒泡排序要慢。
同学的测试代码没有问题, 问题在于排序对象, 其数据是经过random.shuffle来乱序的
- 首先, alist是用range嵌套生成,生成的数据从小到大排列,非常整齐;
- 而这个shuffle会尽量把数据打乱到最混乱的程度,造成数据布局随机度很高;
- 这样, ShortBubbleSort的短路特性就完全失效,还要付出exchanges变量的判断、赋值代价,实测比原始冒泡排序算法要慢不少。
所以排序算法有时候并不存在绝对的优劣, 尤其是时间复杂度相同的算法们
要在特定的应用场合取得最高排序性能的话, 还需要对数据本身进行分析, 针对数据的特性来选择相应排序算法
另外, 除了时间复杂度, 有时候空间复杂度也是需要考虑的关键因素
归并排序时间复杂度O(nlog n),但需要额外一倍的存储空间,快速排序时间复杂度最好的情况是O(nlog n),而且不需要额外存储空间,但“中值”的选择又成为性能的关键,选择不好的话,极端情况性能甚至低于冒泡排序
算法选择不是一个绝对的优劣判断, 需要综合考虑各方面的因素
包括运行环境要求、处理数据对象的特性
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: