抽象数据类型: ADT Graph
抽象数据类型ADT Graph定义如下:
- Graph():创建一个空的图;
- addVertex(vert):将顶点vert加入图中
- addEdge(fromVert, toVert):添加有向边
- addEdge(fromVert, toVert, weight):添加带权的有向边
- getVertex(vKey):查找名称为vKey的顶点
- getVertices():返回图中所有顶点列表
- in:按照vert in graph的语句形式,返回顶点是否存在图中True/False
ADT Graph的实现方法有两种主要形式:
- 邻接矩阵adjacency matrix
- 邻接表adjacency list
- 两种方法各有优劣,需要在不同应用中加以选择
邻接矩阵Adjacency Matrix
矩阵的每行和每列都代表图中的顶点
如果两个顶点之间有边相连, 设定行列值
无权边则将矩阵分量标注为1,或者0,带权边则将权重保存为矩阵分量值
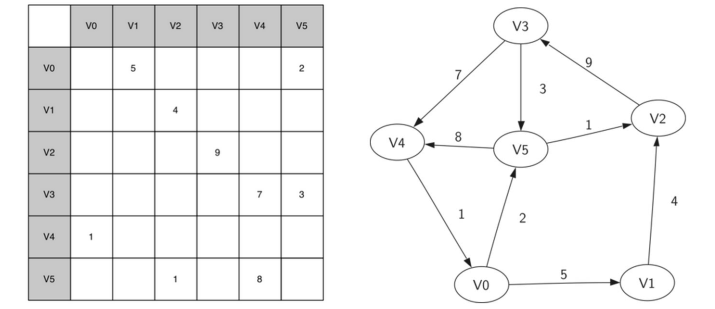
邻接矩阵实现法的优点是简单
可以很容易得到顶点是如何相连
但如果图中的边数很少则效率低下
成为“稀疏sparse”矩阵,而大多数问题所对应的图都是稀疏的边远远少于|V|^2这个量级
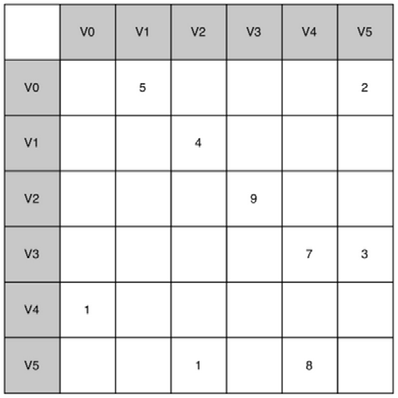
邻接列表Adjacency List
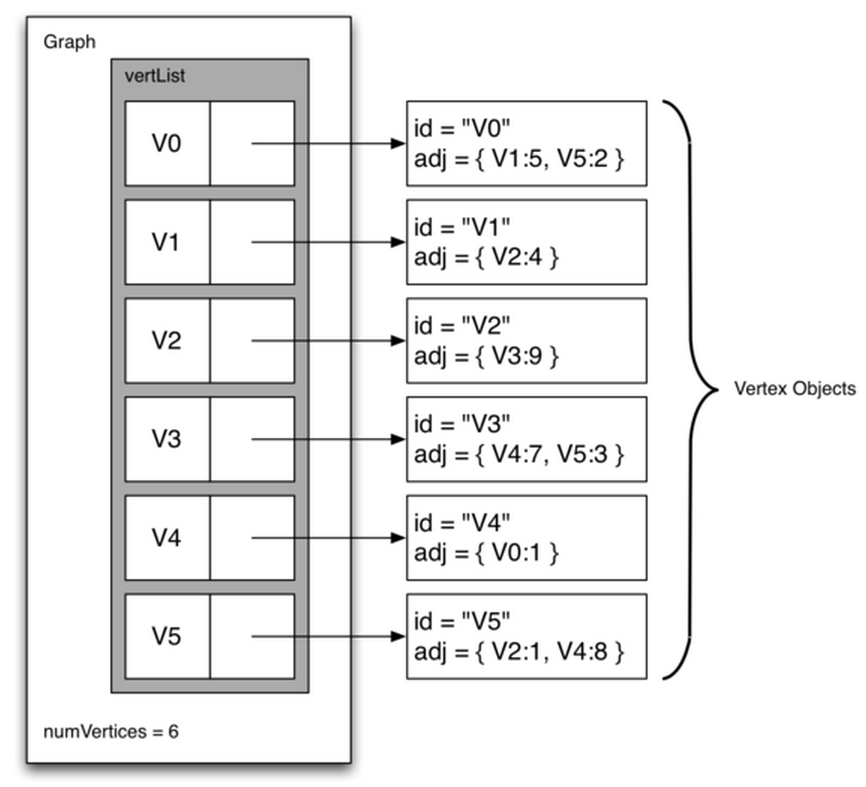
邻接列表adjacency list可以成为稀疏图的更高效实现方案
维护一个包含所有顶点的主列表(master list),主列表中的每个顶点,再关联一个与自身有边连接的所有顶点的列表
邻接列表法的存储空间紧凑高效
很容易获得顶点所连接的所有顶点,以及连接边的信息
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: