复杂递归问题:汉诺塔
传说在一个印度教寺庙里, 有3根柱子, 其中一根套着64个由小到大的黄金盘片, 僧侣们的任务就是要把这一叠黄金盘从一根柱子搬到另一根, 但有两个规则:
一次只能搬1个盘子大盘子不能叠在小盘子上
汉诺塔问题:分解为递归形式
假设我们有5个盘子, 穿在1#柱, 需要挪到3#柱
如果能有办法把最上面的一摞4个盘子统统挪到2#柱,那问题就好解决了:把剩下的最大号盘子直接从1#柱挪到3#柱再用同样的办法把2#柱上的那一摞4个盘子挪到3#柱,就完成了整个移动
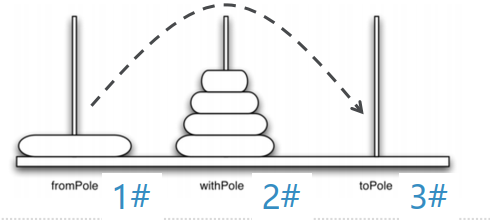
汉诺塔问题:分析
接下来问题就是解决4个盘子如何能从1#挪到2#?
此时问题规模已经减小!同样是想办法把上面的一摞3个盘子挪到3#柱,把剩下最大号盘子从1#挪到2#柱,再用同样的办法把一摞3个盘子从3#挪到2#柱
一摞3个盘子的挪动也照此:
分为上面一摞2个,和下面最大号盘子
那么2个盘子怎么移动?
不行, 就再分解为1个盘子的移动
汉诺塔问题:递归思路
将盘片塔从开始柱, 经由中间柱, 移动到目标柱:
首先将上层N-1个盘片的盘片塔,从开始柱,经由目标柱,移动到中间柱;
然后将第N个(最大的)盘片,从开始柱,移动到目标柱;
最后将放置在中间柱的N-1个盘片的盘片塔,经由开始柱,移动到目标柱。
基本结束条件, 也就是最小规模问题是:
1个盘片的移动问题
上面的思路用Python写出来, 几乎跟语言描述一样:
def moveTower(height, fromPole, withPole, toPole):
if height >= 1:
moveTower(height-1, fromPole, toPole, withPole)
moveDisk(height, fromPole, toPole)
moveTower(height-1, withPole, fromPole, toPole)
def moveDisk(disk, fromPole, toPole):
print(f"Moving disk[{disk}] from {fromPole} to {toPole}")
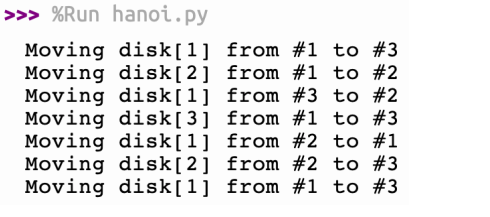
moveTower(3, "#1", "#2", "#3")
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: