35、数据结构与算法Python：谢尔排序算法及分析

谢尔排序Shell Sort

我们注意到插入排序的比对次数， 在最好的情况下是O(n)， 这种情况发生在列表已是有序的情况下， 实际上， 列表越接近有序， 插入排序的比对次数就越少

从这个情况入手， 谢尔排序以插入排序作为基础， 对无序表进行“间隔”划分子列表， 每个子列表都执行插入排序

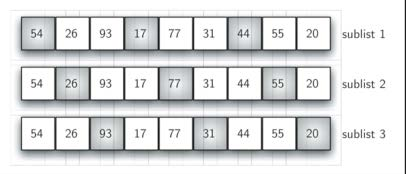
随着子列表的数量越来越少， 无序表的整体越来越接近有序， 从而减少整体排序的比对次数

间隔为3的子列表， 子列表分别插入排序后的整体状况更接近有序

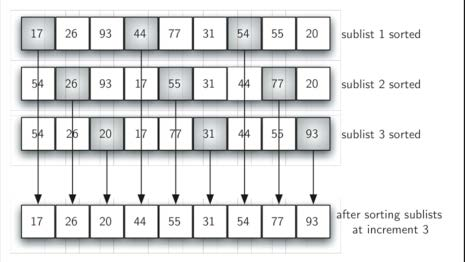
谢尔排序：思路

最后一趟是标准的插入排序， 但由于前面几趟已经将列表处理到接近有序， 这一趟仅需少数几次移动即可完成

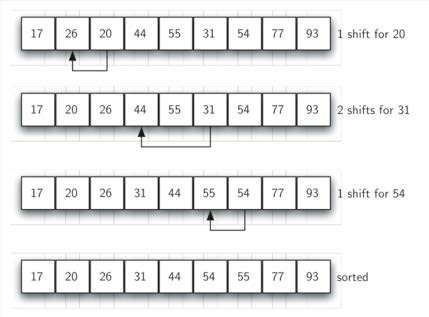
子列表的间隔一般从n/2开始， 每趟倍增： n/4, n/8……直到1

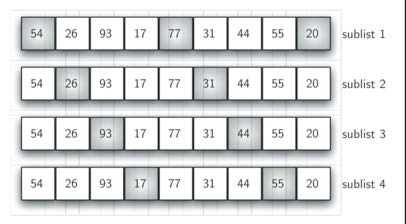
谢尔排序：代码

def shellSort(alist):
    # 间隔设定
    sublistcount = len(alist) // 2
    while sublistcount > 0:
        # 子列表排序
        for startposition in range(sublistcount):
            gapInsertionSort(alist, startposition, sublistcount)
        print("After increments of size", sublistcount, "The list is", alist)

        # 间隔缩小
        sublistcount = sublistcount // 2
def gapInsertionSort(alist, start, gap):
    for i in range(start + gap, len(alist), gap):
        currentvalue = alist[i]
        position = i
        while position >= gap and alist[position - gap] > currentvalue:
            alist[position] = alist[position - gap]
            position = position - gap
        alist[position] = currentvalue
alist = [1, 12, 3, 312, 13, 11, 14]
shellSort(alist)
print(alist)

谢尔排序：算法分析

粗看上去， 谢尔排序以插入排序为基础，可能并不会比插入排序好

但由于每趟都使得列表更加接近有序， 这过程会减少很多原先需要的“无效”比对

对谢尔排序的详尽分析比较复杂，大致说是介于O(n)和O(n^2)之间

如果将间隔保持在2k-1(1、 3、 5、 7、 15、 31等等） ， 谢尔排序的时间复杂度约为O（n^3/2)

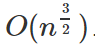
版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: