41、数据结构与算法Python：散列函数设计

散列函数设计：折叠法

折叠法设计散列函数的基本步骤是

将数据项按照位数分为若干段，再将几段数字相加，最后对散列表大小求余，得到散列值

例如， 对电话号码62767255

可以两位两位分为4段（62、 76、 72、 55）
相加（62+76+72+55=265）
散列表包括11个槽，那么就是265%11=1
所以h(62767255)=1

有时候折叠法还会包括一个隔数反转的步骤

比如（62、 76、 72、 55）隔数反转为（62、 67、 72、 55）
再累加（62+67+72+55=256）
对11求余（256%11=3），所以h’(62767255)=3

虽然隔数反转从理论上看来毫无必要， 但这个步骤确实为折叠法得到散列函数提供了一种微调手段， 以便更好符合散列特性

散列函数设计：平方取中法

平方取中法， 首先将数据项做平方运算，然后取平方数的中间两位， 再对散列表的大小求余

例如， 对44进行散列

首先44*44=1936
然后取中间的93
对散列表大小11求余， 93%11=5

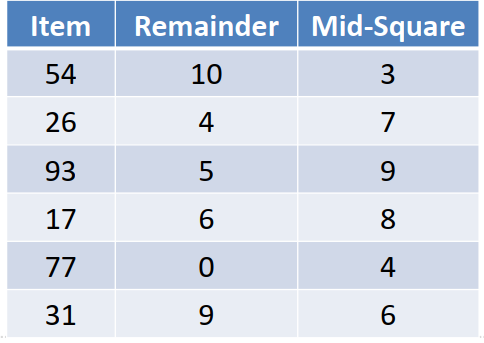
下表是两种散列函数的对比

两个都是完美散列函数
分散度都很好
平方取中法计算量稍大

散列函数设计：非数项

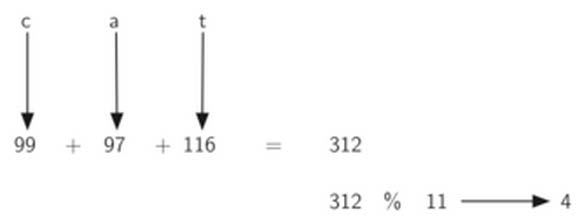
我们也可以对非数字的数据项进行散列，把字符串中的每个字符看作ASCII码即可

如cat， ord(‘c’)==99, ord(‘a’)==96, ord(‘t’)==116

再将这些整数累加， 对散列表大小求余

代码

def hash(astring, tablesize):
    sum = 0
    for pos in range(len(astring)):
        sum = sum + ord(astring[pos])
    
    return sum%tablesize

散列函数设计

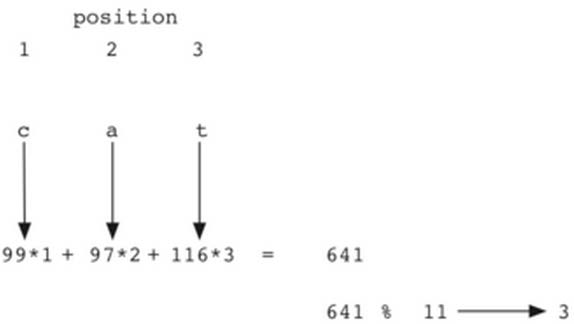
当然， 这样的散列函数对所有的变位词都返回相同的散列值

为了防止这一点，可以将字符串所在的位置作为权重因子，乘以ord值

我们还可以设计出更多的散列函数方法，但要坚持的一个基本出发点是， 散列函数不能成为存储过程和查找过程的计算负担

如果散列函数设计太过复杂， 去花费大量的计算资源计算槽号

可能还不如简单地进行顺序查找或者二分查找

失去了散列本身的意义

版权声明：本文不是「本站」原创文章，版权归原作者所有 | 原文地址: