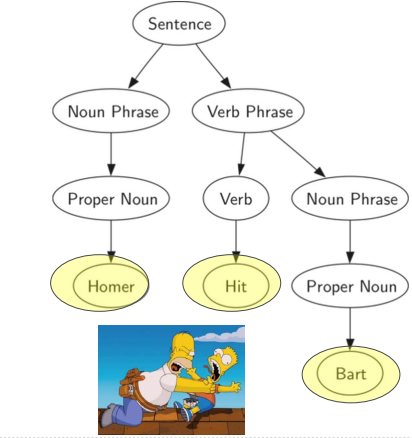
树的应用:解析树(语法树)
将树用于表示语言中句子, 可以分析句子的各种语法成分, 对句子的各种成分进行处理
语法分析树主谓宾,定状补
程序设计语言的编译
词法、语法检查从语法树生成目标代码
自然语言处理
机器翻译、语义理解
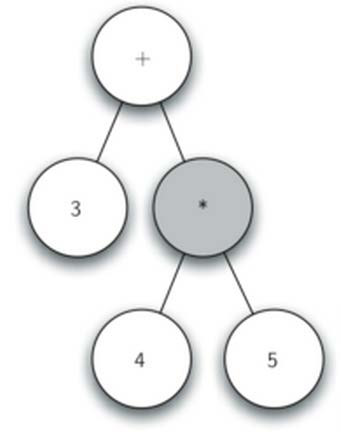
树的应用: 表达式解析
我们还可以将表达式表示为树结构
叶节点保存操作数,内部节点保存操作符
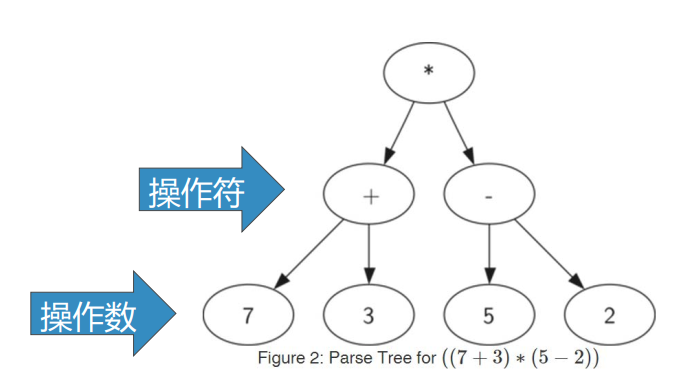
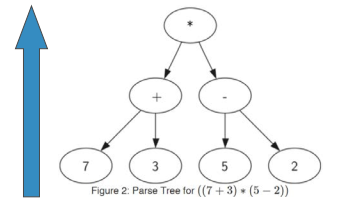
全括号表达式((7+3)*(5-2))
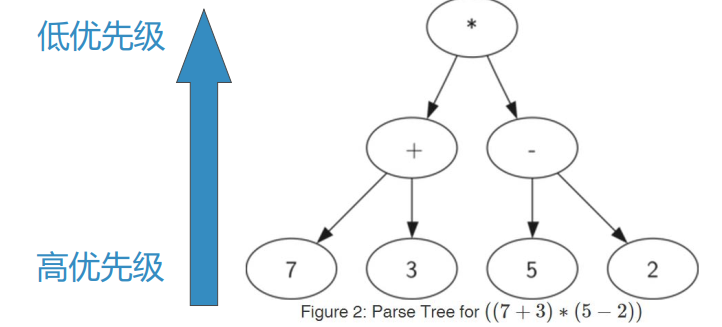
由于括号的存在,需要计算*的话,就必须先计算7+3和5-2,表达式层次决定计算的优先级越底层的表达式,优先级越高
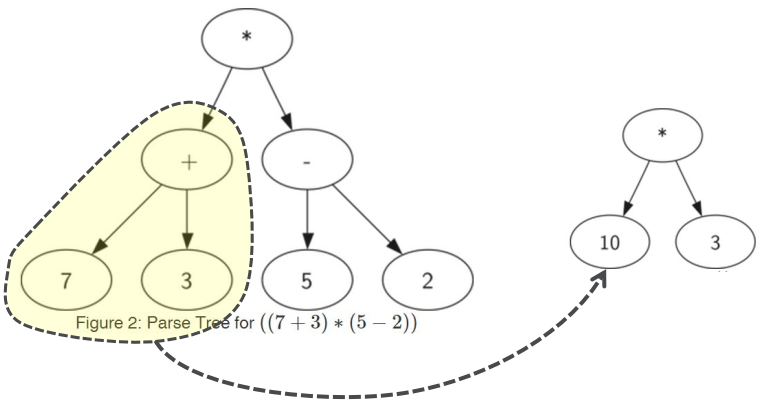
树中每个子树都表示一个子表达式
将子树替换为子表达式值的节点,即可实现求值
表达式解析树
下面, 我们用树结构来做如下尝试
从全括号表达式构建表达式解析树,利用表达式解析树对表达式求值,从表达式解析树恢复原表达式的字符串形式
首先, 全括号表达式要分解为单词Token列表
其单词分为括号“() ”、操作符“**/”和操作数“0~9”这几类,左括号就是表达式的开始,而右括号是表达式的结束
建立表达式解析树:实例
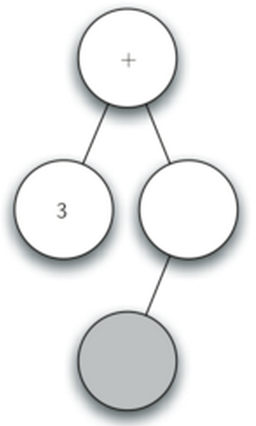
全括号表达式: (3+(4*5))

创建表达式解析树过程
- 创建空树,当前节点为根节点
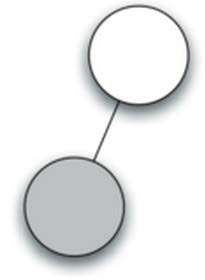
- 读入’(’, 创建了左子节点,当前节点下降
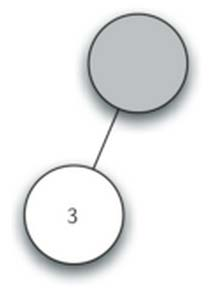
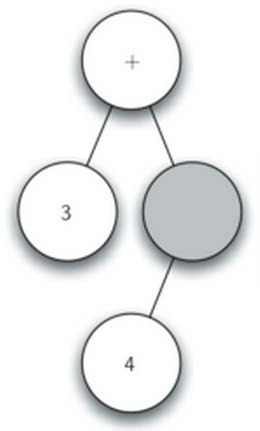
- 读入’3’,当前节点设置为3, 上升到父节点
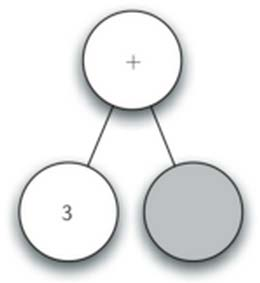
- 读入’+’,当前节点设置为+, 创建右子节点,当前节点下降
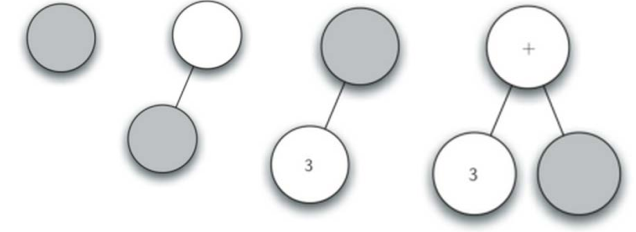
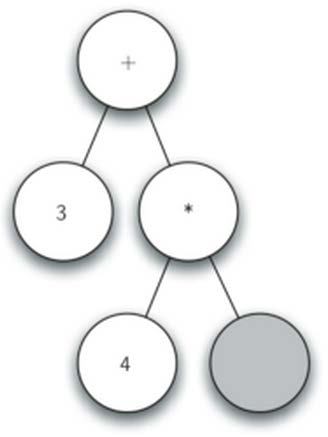
- 读入’(’, 创建左子节点,当前节点下降
- 读入’4’,当前节点设置为4, 上升到父节点
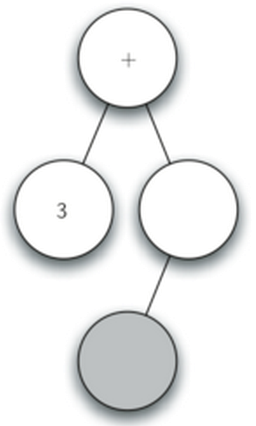
- 读入’’,当前节点设置为, 创建右子节点,当前节点下降
 |
 |
 |
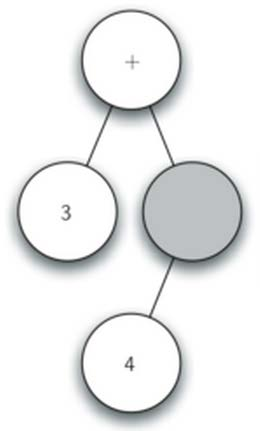
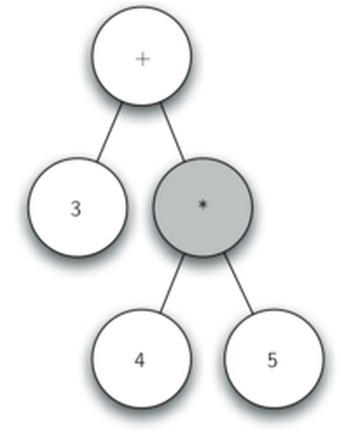
- 读入’5’,当前节点设置为5, 上升到父节点
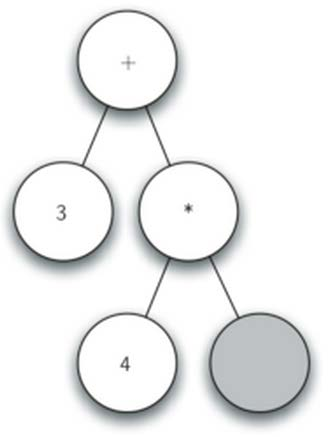
- 读入’)’, 上升到父节点
- 读入’)’,再上升到父节点
建立表达式解析树:规则
从左到右扫描全括号表达式的每个单词,依据规则建立解析树
如果当前单词是"(":为当前节点添加一个新节点作为其左子节点, 当前节点下降为这个新节点。如果当前单词是操符"+,-,/,*":将当前节点的值设为此符号,为当前节点添加一个新节点作为其右子节点, 当前节点下降为这个新节点,如果当前单词是操作数:将当前节点的值设为此数, 当前节点上升到父节点,如果当前单词是")":则当前节点上升到父节点
建立表达式解析树:实例
全括号表达式: (3+(4*5))
 |
 |
 |
 |
 |
 |
 |
 |
建立表达式解析树:思路
从图示过程中我们看到, 创建树过程中关键的是对当前节点的跟踪
- 创建左右子树可调用insertLeft/Right
- 当前节点设置值,可以调用setRootVal
- 下降到左右子树可调用getLeft/RightChild
- 但是, 上升到父节点,这个没有方法支持!
我们可以用一个栈来记录跟踪父节点
- 当前节点下降时,将下降前的节点push入栈
- 当前节点需要上升到父节点时,上升到pop出栈的节点即可!
建立表达式解析树:代码
class BinaryTree:
def __init__(self, rootObj):
self.key = rootObj
self.leftChild = None
self.rightChild = None
def insertLeft(self, newNode):
if self.leftChild == None:
self.leftChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.leftChild = self.leftChild
self.leftChild = t
def insertRight(self, newNode):
if self.rightChild == None:
self.rightChild = BinaryTree(newNode)
else:
t = BinaryTree(newNode)
t.rightChild = self.rightChild
self.rightChild = t
def getRightChild(self):
return self.rightChild
def getLeftChild(self):
return self.leftChild
def setRootVal(self, obj):
self.key = obj
def getRootVal(self):
return self.key
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[-1]
def size(self):
return len(self.items)
def buildParseTree(fpexp):
fplist = fpexp.split()
pStack = Stack()
eTree = BinaryTree('')
# 入栈下降
pStack.push(eTree)
currentTree = eTree
for i in fplist:
# 表达式开始
if i == '(':
currentTree.insertLeft('')
# 入栈下降
pStack.push(currentTree)
currentTree = currentTree.getLeftChild()
# 操作数
elif i not in ['+', '-', '*', '/', ')']:
currentTree.setRootVal(int(i))
# 出栈上升
parent = pStack.pop()
currentTree = parent
# 操作符
elif i in ['+', '-', '*', '/']:
currentTree.setRootVal(i)
currentTree.insertRight('')
pStack.push(currentTree)
currentTree = currentTree.getRightChild()
# 表达式结束
elif i == ')':
# 出栈上升
currentTree = pStack.pop()
else:
raise ValueError
return eTree
创建了表达式解析树, 可用来进行求值
由于二叉树BinaryTree是一个递归数据结构, 自然可以用递归算法来处理
求值递归函数evaluate
由前述对子表达式的描述,可从树的底层子树开始,逐步向上层求值,最终得到整个表达式的值
求值函数evaluate的递归三要素:
- 基本结束条件:叶节点是最简单的子树,没有左右子节点,其根节点的数据项即为子表达式树的值
- 缩小规模:将表达式树分为左子树、右子树,即为缩小规模
- 调用自身:分别调用evaluate计算左子树和右子树的值,然后将左右子树的值依根节点的操作符进行计算,从而得到表达式的值
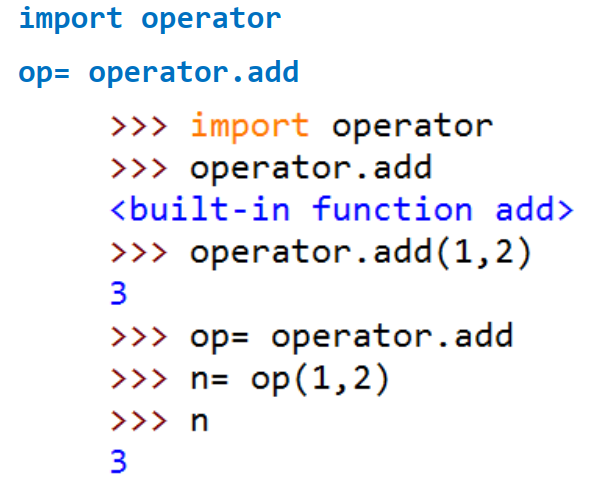
一个增加程序可读性的技巧:函数引用
利用表达式解析树求值:代码
import operator
def evaluate(parseTree):
opers = {
'+': operator.add, '-': operator.sub, '*': operator.mul, '/': operator.truediv}
# 缩小规模
leftC = parseTree.getLeftChild()
rightC = parseTree.getRightChild()
if leftC and rightC:
fn = opers[parseTree.getRootVal()]
# 递归调用
return fn(evaluate(leftC), evaluate(rightC))
else:
# 基本结束条件
return parseTree.getRootVal()
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: