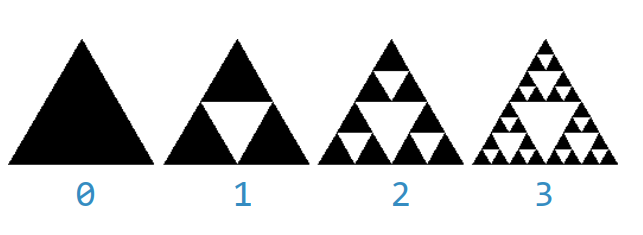
谢尔宾斯基Sierpinski三角形
分形构造, 平面称谢尔宾斯基三角形, 立体称谢尔宾斯基金字塔
谢尔宾斯基三角形:作图思路
根据自相似特性, 谢尔宾斯基三角形是由3个尺寸减半的谢尔宾斯基三角形按照品字形拼叠而成
由于我们无法真正做出谢尔宾斯基三角形(degree->∞),只能做degree有限的近似图形。
代码
import turtle
def sierpinski(degree, points):
colormap = ['blue', 'red', 'green', 'white', 'yellow', 'orange']
# 等边三角形
drawTriangle(points, colormap[degree])
# 最小规模,0直接退出
if degree > 0:
# 减小规模 getMid边长减半
# 调用自身,左上右次序
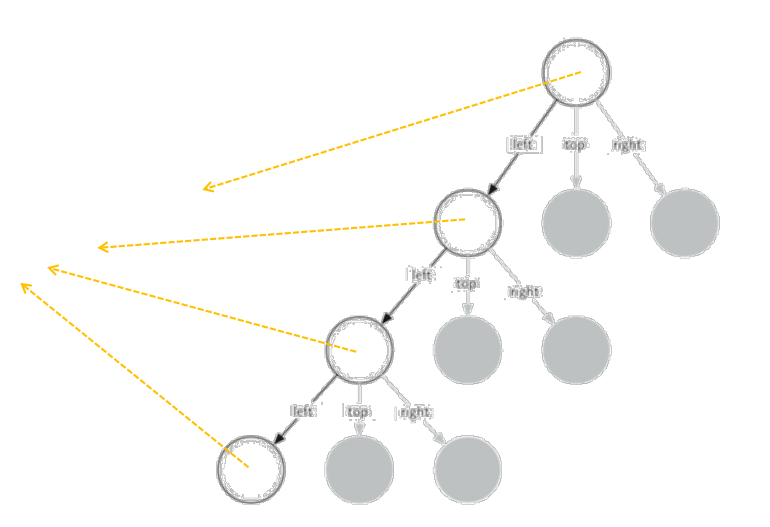
sierpinski(degree - 1, {
'left': points['left'],
'top': getMid(points['left'], points['top']),
'right': getMid(points['left'], points['right'])})
sierpinski(degree - 1, {
'left': getMid(points['left'], points['top']),
'top': points['top'],
'right': getMid(points['top'], points['right'])})
sierpinski(degree - 1, {
'left': getMid(points['left'], points['right']),
'top': getMid(points['top'], points['right']),
'right': points['right']})
# 绘制等边三角形
def drawTriangle(points, color):
t.fillcolor(color)
t.penup()
t.goto(points['top'])
t.pendown()
t.begin_fill()
t.goto(points['left'])
t.goto(points['right'])
t.goto(points['top'])
t.end_fill()
def getMid(p1, p2):
return ((p1[0] + p2[0]) / 2, (p1[1] + p2[1]) / 2)
t = turtle.Turtle()
points = {
'left': (-200, -100),
'top': (0, 200),
'right': (200, -100),
}
sierpinski(5, points)
turtle.done()

degree=3的绘制过程
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: