数据结构与算法38-鸭棋
题目描述
题目背景
鸭棋是一种风靡鸭子界的棋类游戏。事实上,它与中国象棋有一些相似之处,但规则不尽相同。在这里,我们将为你介绍鸭棋的规则。
同时,我们下发了一个模拟鸭棋规则的玩具,你可以结合这个玩具理解题目(也可以在 AK 后与你的队友进行对弈)。详情请见「玩具使用说明」。
鸭棋在一个 10 * 9 10\times 9 10*9( 10 10 10 行 9 9 9 列)的网格棋盘上进行,网格上的每个格点都可以有棋子停留。对弈双方一方执红(red)棋、另一方执蓝(blue)棋,双方轮流执行操作,轮到一位玩家操作时,他必须选择一枚自己的棋子,并按照规则进行一步移动。
鸭棋发明者鸭子德规定一局鸭棋由红方执先手,并设计了初始棋盘布局如下:
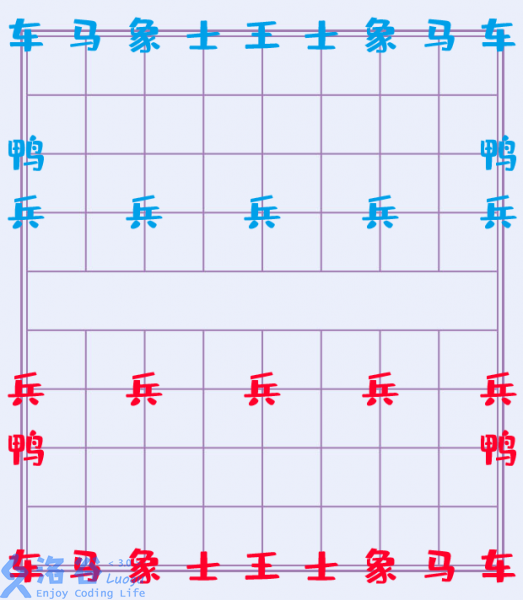
棋子类型与走子规则
棋子分为 7 7 7 类,下面介绍了它们的名字以及它们的移动规则。介绍移动规则时,我们默认棋子所处位置为 ( x , y ) \left( x,y\right) (x,y)(表示第 x x x 行的第 y y y 列,下同),并列出它可以到达的位置:
-
王(captain):可达的位置共 4 4 4 个,包括 ( x * 1 , y ) \left(x\pm 1,y\right) (x*1,y) 及 ( x , y * 1 ) \left(x,y\pm 1\right) (x,y*1)。
-
士(guard):可达的位置共 4 4 4 个,包括 ( x * 1 , y * 1 ) \left(x\pm 1,y\pm 1\right) (x*1,y*1) 及 ( x * 1 , y ∓ 1 ) \left(x\pm 1,y\mp 1\right) (x*1,y∓1)。
-
象(elephant):可达的位置至多 4 4 4 个,对于任意 s x , s y ∈ { 1 , − 1 } s_x,s_y\in \left\{ 1,-1\right\} sx,sy∈{ 1,−1},分别有:
-
如果位置 ( x + s x * 1 , y + s y * 1 ) \left(x+s_x\times 1 ,y+ s_y\times 1\right) (x+sx*1,y+sy*1) 上无任意一方的棋子停留,则 ( x + s x * 2 , y + s y * 2 ) \left( x+s_x \times 2,y+s_y \times 2\right) (x+sx*2,y+sy*2) 为一个可达的位置。
-
马(horse):可达的位置至多 8 8 8 个,对于任意 s x , s y ∈ { 1 , − 1 } s_x,s_y\in \left\{ 1,-1\right\} sx,sy∈{ 1,−1},分别有:
-
如果位置 ( x + s x * 1 , y ) \left(x+s_x\times 1 ,y\right) (x+sx*1,y) 上无任意一方的棋子停留,则 ( x + s x * 2 , y + s y * 1 ) \left( x+s_x \times 2,y+s_y \times 1\right) (x+sx*2,y+sy*1) 为一个可达的位置。
-
如果位置 ( x , y + s y * 1 ) \left(x ,y+ s_y \times 1 \right) (x,y+sy*1) 上无任意一方的棋子停留,则 ( x + s x * 1 , y + s y * 2 ) \left( x+s_x \times 1,y+s_y \times 2\right) (x+sx*1,y+sy*2) 为一个可达的位置。
-
车(car):可在不跨越其他棋子的前提下,到达同行或同列的所有其他位置。
-
鸭(duck):可达的位置至多 8 8 8 个,对于任意 s x , s y ∈ { 1 , − 1 } s_x,s_y\in \left\{ 1,-1\right\} sx,sy∈{ 1,−1},分别有:
-
如果位置 ( x + s x * 2 , y + s y * 1 ) , ( x + s x * 1 , y ) \left(x+s_x\times 2 ,y+s_y \times 1\right),\left(x+s_x\times 1 ,y\right) (x+sx*2,y+sy*1),(x+sx*1,y) 上均无任意一方的棋子停留,则 ( x + s x * 3 , y + s y * 2 ) \left( x+s_x \times 3,y+s_y \times 2\right) (x+sx*3,y+sy*2) 为一个可达的位置。
-
如果位置 ( x + s x * 1 , y + s y * 2 ) , ( x , y + s y * 1 ) \left(x+s_x \times 1 ,y+ s_y \times 2 \right),\left(x ,y+ s_y \times 1 \right) (x+sx*1,y+sy*2),(x,y+sy*1) 上均无任意一方的棋子停留,则 ( x + s x * 2 , y + s y * 3 ) \left( x+s_x \times 2,y+s_y \times 3\right) (x+sx*2,y+sy*3) 为一个可达的位置。
-
兵(soldier):可达的位置共 8 8 8 个,包括 ( x * 1 , y ) \left(x\pm 1,y\right) (x*1,y) 及 ( x , y * 1 ) \left(x,y\pm 1\right) (x,y*1) 及 ( x * 1 , y * 1 ) \left(x\pm 1,y\pm 1\right) (x*1,y*1) 及 ( x * 1 , y ∓ 1 ) \left(x\pm 1,y\mp 1\right) (x*1,y∓1)。
除上面描述的规则之外,棋子移动还有如下额外规则:
- 不能将棋子移动到棋盘外的某个位置。
- 玩家不能将棋子移动到已经停留了己方棋子的位置。
- 如果玩家将棋子移动到了一个已经停留了对方棋子的位置,那么原本停留在该位置上的这个对方棋子将被移出游戏。
胜利条件与将军局面
玩家在这个游戏中的目标是将对方的王移出游戏。一旦一方的王被移出游戏,则另一方立即宣告胜利。
对于一个棋盘的状态,如果存在一方有一步合法的操作能够将另一方的王移出游戏,则我们说当前局面是一个将军的局面。需要友情提示的是,根据定义,将军局面的形成包括(但不限于)如下这些可能:
1、 一方将一枚棋子移动到可以攻击对方王的位置;
2、 在己方王受到威胁时不采取措施躲避;
3、 主动将王移动至会受到攻击的位置;
除此之外,需要特别说明的是,游戏结束后,由于双方不可再操作,因此不可能出现将军局面,即便此时另一方王处于被「攻击」的位置。
题目描述
今年的IDCC(International Duck Chess Competition,国际鸭棋大赛)正在如火如荼地进行着。你观摩了一场精彩绝伦的比赛,但你对对弈过程的记忆已经模糊不清了,只有系统留下的他们的操作序列,序列中的每个操作为当前操作者试图移动某个位置的棋子至另一个位置。你希望用这个序列,来复现出整局棋局的对弈过程。即,对于每步操作,你需要首先判其是否合法,若合法,则进一步求出:
1、 这步操作移动了哪个棋子;
2、 这步操作后,是否存在棋子被移出游戏,如有则还需求出被移出游戏的棋子;
3、 这步操作后,是否形成将军局面;
4、 这步操作后,游戏是否结束;
可能包含的不合法情况如下:
- 此步移动的初始位置无己方棋子停留。
- 此步移动的初始位置有己方棋子停留,但移动不符合规则。
- 游戏已经结束。
序列中的不合法操作是需要被忽略的。比如,如果轮到红方移动,此时序列中的当前操作恰好是不合法的,则这个操作将被忽略,序列中的下一步操作将成为红方这步的操作(如仍不合法则继续忽略,直至出现合法的操作)。
输入格式
第一行一个非负整数 Q Q Q,表示操作序列的长度。接下来依次描述每个操作。
接下来 Q Q Q 行,每行 4 4 4 个整数 x s , y s , x t , y t x_s, y_s, x_t, y_t xs,ys,xt,yt( 0 ≤ x s , x t < 10 0\leq x_s,x_t < 10 0≤xs,xt<10, 0 ≤ y s , y t < 9 0\leq y_s,y_t < 9 0≤ys,yt<9),描述一个欲将 ( x s , y s ) \left(x_s,y_s\right) (xs,ys) 处棋子移动到 ( x t , y t ) \left(x_t,y_t\right) (xt,yt) 的操作。在这里,我们规定左下角(即红方车摆放的位置,图见「题目背景」)为 ( 0 , 0 ) \left(0,0\right) (0,0)。
保证Q ≤ 1000 Q\leq 1000 Q≤1000。
输出格式
输出Q Q Q 行,对于每个操作依次输出复现结果。每行输出一个操作的结果:
-
如果该操作为不合法操作,则请输出 Invalid command。
-
如果为合法操作,则依次回答「题目描述」中的问题 1 ∼ 4 1\sim 4 1∼4:
-
被移动的棋子用
[颜色] [类型](注意中间包含空格)来描述,请使用它们的英文名称(见「题目背景」)。如,红象为red elephant,蓝王为blue captain。 -
被移出游戏的棋子的描述方式与上面类似。特别地,如果无棋子被移出游戏,则该问题的答案为
NA。 -
用
yes、no分别表示形成、不形成将军局面。 -
用
yes、no分别表示游戏结束、游戏不结束。 -
用
;(分号)将所有问题的答案隔开。 -
比如,四个问题的答案分别为:被移动的棋子是蓝车,无棋子被移出游戏,形成将军局面,游戏未结束。则该行应输出
blue car;NA;yes;no。
样例
样例输入
18
00 7 0
90 8 0
01 1 3
02 2 0
03 1 2
04 0 3
94 8 4
32 2 3
70 4 2
70 5 3
92 7 4
20 4 3
91 8 3
43 6 6
74 9 2
84 9 4
66 9 4
98 8 8
样例输出
Invalid command
Invalid command
Invalid command
Invalid command
red guard;NA;no;no
Invalid command
blue captain;NA;no;no
red soldier;NA;no;no
Invalid command
Invalid command
blue elephant;NA;no;no
red duck;NA;no;no
blue horse;NA;no;no
red duck;blue soldier;no;no
Invalid command
blue captain;NA;yes;no
red duck;blue captain;no;yes
Invalid command
参考程序
# 定义棋盘初始状态,正数代表红棋,负数代表蓝棋
chess_board = [[5, 4, 3, 2, 1, 2, 3, 4, 5],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[6, 0, 0, 0, 0, 0, 0, 0, 6],
[7, 0, 7, 0, 7, 0, 7, 0, 7],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[-7, 0, -7, 0, -7, 0, -7, 0, -7],
[-6, 0, 0, 0, 0, 0, 0, 0, -6],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[-5, -4, -3, -2, -1, -2, -3, -4, -5]]
# 定义红方和蓝方当前拥有的棋子和棋子的位置:三元组表示棋子号、位置横坐标、纵坐标
red_chess = [[5, 0, 0], [4, 0, 1], [3, 0, 2], [2, 0, 3], [1, 0, 4], [2, 0, 5], [3, 0, 6], [4, 0, 7], [5, 0, 8],
[6, 2, 0], [6, 2, 8],
[7, 3, 0], [7, 3, 2], [7, 3, 4], [7, 3, 6], [7, 3, 8]]
blue_chess = [[-5, 9, 0], [-4, 9, 1], [-3, 9, 2], [-2, 9, 3], [-1, 9, 4], [-2, 9, 5], [-3, 9, 6], [-4, 9, 7],
[-5, 9, 8],
[-6, 7, 0], [-6, 7, 8],
[-7, 6, 0], [-7, 6, 2], [-7, 6, 4], [-7, 6, 6], [-7, 6, 8]]
def JudgeBound(x, y):
# 判断棋子是否位于棋盘内部
return x >= 0 and x < 10 and y >= 0 and y < 9
def abs(x):
if x < 0:
return -x
return x
def OutputChess(x, y):
dic = {
1: 'captain', 2: 'guard', 3: 'elephant', 4: 'horse', 5: 'car', 6: 'duck', 7: 'soldier'}
if chess_board[x][y] > 0:
return "red " + dic[chess_board[x][y]]
elif chess_board[x][y] < 0:
vis = -chess_board[x][y]
return 'blue ' + dic[vis]
def GetNextHop(kind_no, x, y):
nextStepList = []
s = [1, -1]
if abs(kind_no) == 1:
add = [1, -1]
for dx in add:
if JudgeBound(x + dx, y):
nextStepList.append([x + dx, y])
for dy in add:
if JudgeBound(x, y + dy):
nextStepList.append([x, y + dy])
elif abs(kind_no) == 2:
add = [1, -1]
for dx in add:
for dy in add:
if JudgeBound(x + dx, y + dy):
nextStepList.append([x + dx, y + dy])
for dx in add:
for dy in add[::-1]:
if JudgeBound(x + dx, y + dy):
nextStepList.append([x + dx, y + dy])
elif abs(kind_no) == 3:
for sx in s:
for sy in s:
if JudgeBound(x + sx, y + sy) and chess_board[x + sx][y + sy] == 0 and JudgeBound(x + sx * 2,
y + sy * 2):
nextStepList.append([x + sx * 2, y + sy * 2])
elif abs(kind_no) == 4:
for sx in s:
for sy in s:
if JudgeBound(x + sx, y) and chess_board[x + sx][y] == 0 and JudgeBound(x + sx * 2, y + sy * 1):
nextStepList.append([x + sx * 2, y + sy])
if JudgeBound(x, y + sy) and chess_board[x][y + sy] == 0 and JudgeBound(x + sx, y + sy * 2):
nextStepList.append([x + sx, y + sy * 2])
elif abs(kind_no) == 5:
# 兵,可在不跨越其他棋子的前提下,到达同行或同列的所有其他位置。注意是“不跨越”,如果按照某个方向走,初次遇到一个棋子,
# 那么这个棋子的位置也是可达的!并不一定没有棋子的位置才是可达的
dx = 1
while JudgeBound(x - dx, y):
if chess_board[x - dx][y] == 0:
nextStepList.append([x - dx, y])
else:
nextStepList.append([x - dx, y])
break
dx += 1
dx = 1
while JudgeBound(x + dx, y):
if chess_board[x + dx][y] == 0:
nextStepList.append([x + dx, y])
else:
nextStepList.append([x + dx, y])
break
dx += 1
dy = 1
while JudgeBound(x, y + dy):
if chess_board[x][y + dy] == 0:
nextStepList.append([x, y + dy])
else:
nextStepList.append([x, y + dy])
break
dy += 1
dy = 1
while JudgeBound(x, y - dy):
if chess_board[x][y - dy] == 0:
nextStepList.append([x, y - dy])
else:
nextStepList.append([x, y - dy])
break
dy += 1
elif abs(kind_no) == 6:
for sx in s:
for sy in s:
if JudgeBound(x + sx * 2, y + sy) and JudgeBound(x + sx, y) and chess_board[x + sx * 2][y + sy] == 0 and \
chess_board[x + sx][y] == 0 and JudgeBound(x + sx * 3, y + sy * 2):
nextStepList.append([x + sx * 3, y + sy * 2])
if JudgeBound(x + sx, y + sy * 2) and JudgeBound(x, y + sy) and chess_board[x + sx][y + sy * 2] == 0 and \
chess_board[x][y + sy] == 0 and JudgeBound(x + sx * 2, y + sy * 3):
nextStepList.append([x + sx * 2, y + sy * 3])
elif abs(kind_no) == 7:
add_x = [1, -1]
for dx in add_x:
for dy in [0, 1, -1]:
if JudgeBound(x + dx, y + dy):
nextStepList.append([x + dx, y + dy])
for dy in [1, -1]:
if JudgeBound(x, y + dy):
nextStepList.append([x, y + dy])
return nextStepList
def outputChessboard():
for i in range(0, 10, 1):
print(chess_board[i])
def CheckGeneral():
# 判断将军局面。注意审题:存在一方有一步合法的操作能够将另一方的王移出游戏,则我们说当前局面是一个将军的局面。
# 这并不限制是哪一方,例如即便当前是红方合法操作完,下一步红方的某个棋子的某一步如果会移除蓝方的captain,那么这
# 也是将军局面,而不是只判断下一步蓝方会不会移除红方的captain
for chess in red_chess: # 先判断蓝色captain会不会被kill
next_hop = GetNextHop(chess[0], chess[1], chess[2])
for pos in next_hop:
if chess_board[pos[0]][pos[1]] == -1:
return True
for chess in blue_chess:
next_hop = GetNextHop(chess[0], chess[1], chess[2])
for pos in next_hop:
if chess_board[pos[0]][pos[1]] == 1:
return True
return False
def CheckGameOver():
find = 0
for chess in red_chess: # 先判断红色的captain是否还在
if chess[0] == 1:
find += 1
break
if find == 0:
return True
else:
for chess in blue_chess:
if chess[0] == -1:
find += 1
break
if find == 1:
return True
return False
Q = int(input())
valid_op_cnt = 0
game_over = False
for q in range(Q):
s_x, s_y, e_x, e_y = map(int, input().split())
res = ""
if not (JudgeBound(s_x, s_y) and JudgeBound(e_x, e_y)) or game_over == True:
res = "Invalid command"
else:
if chess_board[s_x][s_y] == 0:
res = "Invalid command"
else:
if (valid_op_cnt % 2 == 0 and chess_board[s_x][s_y] < 0) or (
valid_op_cnt % 2 == 1 and chess_board[s_x][s_y] > 0):
# 应该红方操作但使用的是蓝棋 或者 应该是蓝方操作但使用的是红棋
res = "Invalid command"
else:
mabey_next_hop = GetNextHop(chess_board[s_x][s_y], s_x, s_y)
if [e_x, e_y] not in mabey_next_hop:
res = "Invalid command"
else:
if chess_board[s_x][s_y] * chess_board[e_x][e_y] > 0:
res = "Invalid command"
else:
# 合法操作
if chess_board[s_x][s_y] * chess_board[e_x][e_y] == 0: # 终点没有棋子
res += OutputChess(s_x, s_y) + ';NA;'
if chess_board[s_x][s_y] > 0:
change = red_chess.index([chess_board[s_x][s_y], s_x, s_y])
red_chess[change] = [chess_board[s_x][s_y], e_x, e_y]
else:
change = blue_chess.index([chess_board[s_x][s_y], s_x, s_y])
blue_chess[change] = [chess_board[s_x][s_y], e_x, e_y]
chess_board[e_x][e_y] = chess_board[s_x][s_y]
chess_board[s_x][s_y] = 0
else: # chess_board[s_x][s_y]*chess_board[e_x][e_y]<0:#kill
res += OutputChess(s_x, s_y) + ';' + OutputChess(e_x, e_y) + ';'
los = [chess_board[e_x][e_y], e_x, e_y]
win = [chess_board[s_x][s_y], s_x, s_y]
if chess_board[e_x][e_y] < 0:
blue_chess.remove(los)
# 将蓝棋子移除
win_index = red_chess.index(win)
red_chess[win_index] = [chess_board[s_x][s_y], e_x, e_y]
# 红棋子移动后更新位置信息
else:
red_chess.remove(los)
win_index = blue_chess.index(win)
blue_chess[win_index] = [chess_board[s_x][s_y], e_x, e_y]
chess_board[e_x][e_y] = chess_board[s_x][s_y]
chess_board[s_x][s_y] = 0
# 更新棋盘状态
valid_op_cnt += 1
if CheckGameOver():
# 如果游戏结束,由于双方不可再操作,因此不可能出现将军局面,无需再判断将军局面
res += 'no;yes'
game_over = True
else:
if CheckGeneral():
res += 'yes;no'
else:
res += 'no;no'
print(res)
解题提示
1、 本题不需要复杂的算法,直接模拟问题求解;
2、 特别注意审题:①“兵”的走子规则;②将军局面的判别;③游戏结束和将军局面的关系;
3、 使用python语言解题便于问题抽象模拟,代码相对于C/C++简短,可读性好;
4、 测试用例下载:https://download.csdn.net/download/jialChen/86776422,或者私信;
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: