Description
请定一个无向图,顶点编号从0到n-1,用深度优先搜索(DFS),遍历并输出。遍历时,先遍历节点编号小的。
Input
输入第一行为整数n(0 < n < 100),表示数据的组数。 对于每组数据,第一行是两个整数k,m(0 < k < 100,0 < m < k*k),表示有m条边,k个顶点。 下面的m行,每行是空格隔开的两个整数u,v,表示一条连接u,v顶点的无向边。
Output
输出有n行,对应n组输出,每行为用空格隔开的k个整数,对应一组数据,表示DFS的遍历结果。
Sample Input

Sample Output

(一)基于邻接矩阵的无向图DFS
参考程序
#include <stdio.h>
#define LEN 100
int Map[LEN+5][LEN+5],VisitList[LEN+5],VTable[LEN+5];
//全局变量参数说明: Map的邻接矩阵; VisitList遍历序列; VTable访问标志数组
void CreateMatrix(int PointAmount,int EdgeAmount)
{
int a,b;
while(EdgeAmount--)
{
scanf("%d%d",&a,&b);
Map[a][b]=1;
Map[b][a]=1;
}
}
int cnt,SP;
//全局变量参数说明: cnt访问结点的个数;SP栈顶指针
void DFS_Visit(int start,int PointAmount)
{
int i,j;
if(cnt!=PointAmount)
{
if(VTable[start]==0)
{
VisitList[cnt++]=start;
VTable[start]=1;
SP=cnt-1;
for(i=0;i<PointAmount;i++)
{
Map[i][start]=0;
}
}
for(j=0;j<PointAmount;j++)
{
if(Map[start][j]==1)
{
break;
}
}
if(j==PointAmount)
{
DFS_Visit(VisitList[--SP],PointAmount);
}
else
{
DFS_Visit(j,PointAmount);
}
}
}
void OutputArray(int n,int a[])
{
int i;
for(i=0;i<=n-2;i++)
{
printf("%d ",a[i]);
}
printf("%d\n",a[i]);
}
void RefreshArray(int n,int a[])
{
int i;
for(i=0;i<=n-1;i++)
{
a[i]=0;
}
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int k,m,t;
scanf("%d%d",&k,&m);
CreateMatrix(k,m);
RefreshArray(k,VTable);
cnt=0,SP=0;
DFS_Visit(0,k);
OutputArray(k,VisitList);
}
return 0;
}
/*For Test
1
4 4
0 1
0 2
0 3
2 3
*/
分析:
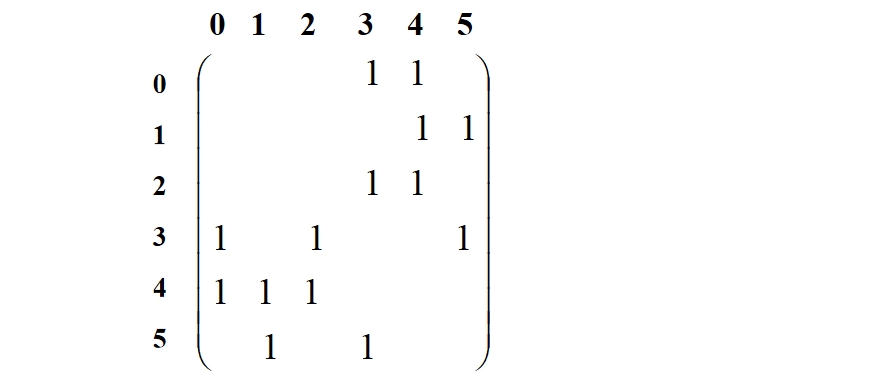
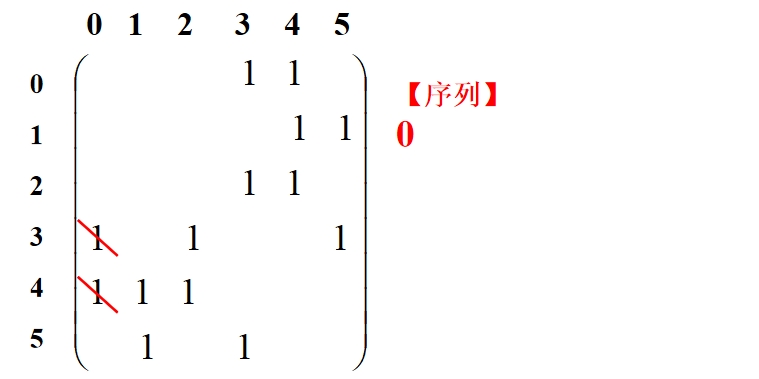
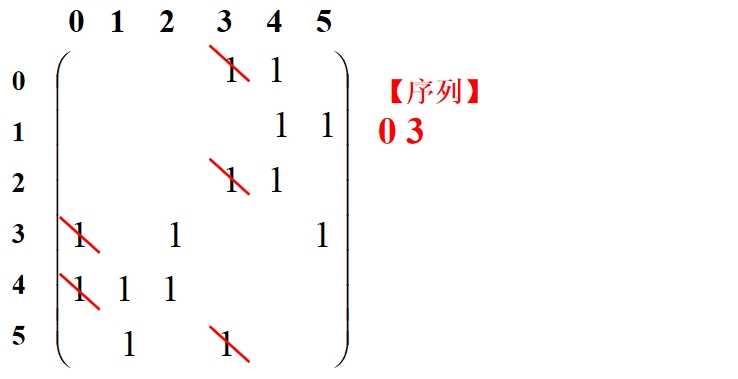
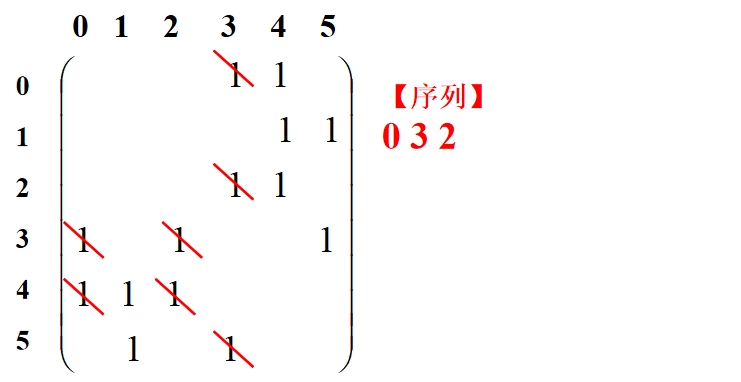
DFS遍历的过程(函数DFS_Visit)简述:①接收一个点start,首先判断此时访问的结点个数cnt是否和结点总数相等,相等则函数结束;否则进行下一步;②判断该结点是否被访问过,即到VTable数组中,检查VTable[start]是否为1,为1表示访问过,为0表示没有访问过。若没有访问,则将start结点加入遍历序列数组VisitList,VTable[start]赋为1,确定栈顶元素的下标SP,然后到邻接矩阵中,将start列所有元素置0,表示不会有结点到达该start点,这样保证了不会重复访问start点;③访问过后,包括原来已经访问过,都要再查找start行,检查是否有以start为起点的邻接点,找到最小的,递归遍历。若没有找到,则进入④;④以栈顶的前一个元素为下一次访问的起点,递归遍历。
这里要注意:访问数组VTable每处理一组数据之前都要预先清零,原因是访问数组VTable不是从0开始赋值的,而是随机访问,所以上一组的VTable结果如果不清零,会影响这一组。而VisitList则无需清零,原因是每一组数据,VisitList的赋值都是从0开始,到PointAmount结束按顺序存储,即便一开始有值,也会被后来新的数据覆盖掉。
下图展示遍历过程:

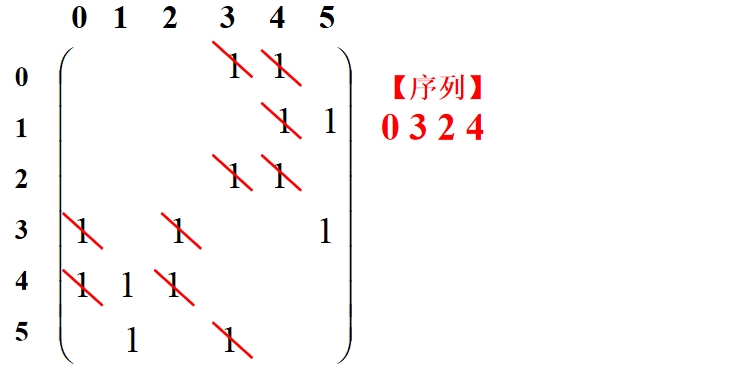
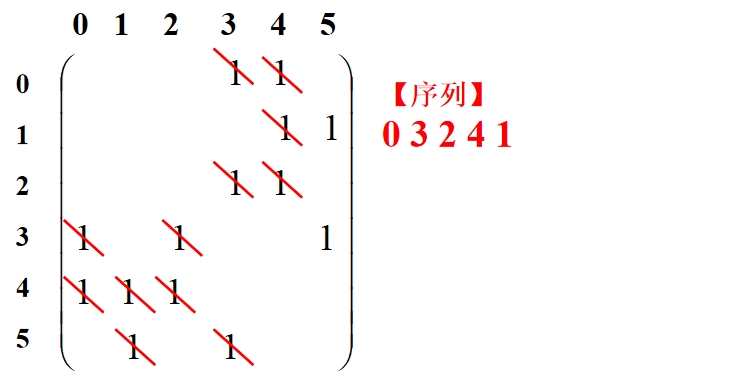
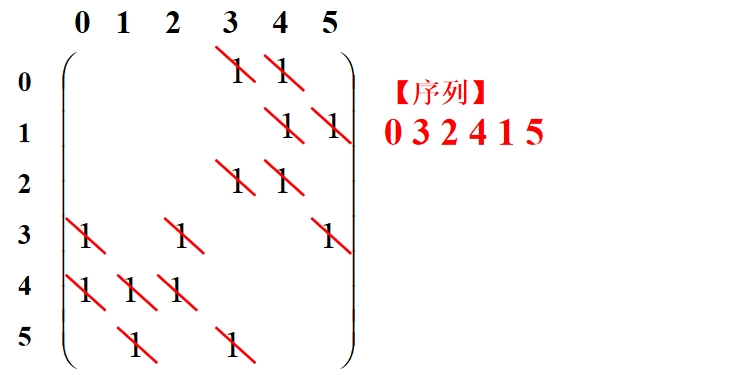
(二)基于邻接链表的无向图DFS
参考程序
#include <stdio.h>
#include <stdlib.h>
#define ROOM sizeof(struct MapNode)
#define LEN 100
struct MapNode
{
int data;
struct MapNode *next;
};
struct MapNode MapList[LEN];
int VisitList[LEN],VisitTable[LEN];
int cnt,SP;
void InsertNode(int a,int x)
{
struct MapNode *p,*p1,*p2;
p2=&MapList[a];
p=(struct MapNode*)malloc(ROOM);
p->data=x;
p->next=NULL;
if(p2->next==NULL)
{
p2->next=p;
}
else
{
p1=p2->next;
while(p1)
{
if(x<p1->data)
{
p->next=p2->next;
p2->next=p;
break;
}
else
{
p2=p1;
p1=p1->next;
}
}
if(p1==NULL)
{
p2->next=p;
}
}
}
void CreateLinkMap(int PointAmount,int EdgeAmount)
{
int a,b;
while(EdgeAmount--)
{
scanf("%d%d",&a,&b);
InsertNode(a,b);
InsertNode(b,a);
}
}
void DeleteNode(int row_num,int target)
{
struct MapNode *p1,*p2;
p2=&MapList[row_num];
if(p2->next)
{
p1=p2->next;
while(p1)
{
if(p1->data==target)
{
p2->next=p1->next;
break;
}
else
{
p2=p1;
p1=p1->next;
}
}
}
}
void DFS_Visit(int start,int PointAmount)
{
int i;
struct MapNode *p;
if(cnt!=PointAmount)
{
if(VisitTable[start]==0)
{
VisitList[cnt++]=start;
VisitTable[start]=1;
SP=cnt-1;
for(i=0;i<PointAmount;i++)
{
DeleteNode(i,start);
}
}
p=&MapList[start];
if(p->next)
{
p=p->next;
DFS_Visit(p->data,PointAmount);
}
else
{
DFS_Visit(VisitList[--SP],PointAmount);
}
}
}
void OutputArray(int PointAmount,int a[])
{
int i;
for(i=0;i<=PointAmount-2;i++)
{
printf("%d ",a[i]);
}
printf("%d\n",a[i]);
}
void RefreshArray(int n,int a[])
{
int i;
for(i=0;i<=n-1;i++)
{
a[i]=0;
}
}
int main()
{
int n;
scanf("%d",&n);
while(n--)
{
int k,m;
scanf("%d%d",&k,&m);
CreateLinkMap(k,m);
cnt=0,SP=0;
RefreshArray(k,VisitTable);
DFS_Visit(0,k);
OutputArray(k,VisitList);
}
return 0;
}
基于链表存储的图的DFS遍历与基于邻接矩阵的图算法相同,不同之处就是涉及到结点的删除操作,而且查找start的邻接结点时,无需查找一行,取出链表第一个数据结点(如果有的话)就是满足要求的结点。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: