【例1】
Description
在2*n的一个长方形方格中,用一个1*2的骨牌铺满方格,输入n ,输出铺放方案的总数. 例如n=3时,为2*3方格,骨牌的铺放方案有三种,如下图:
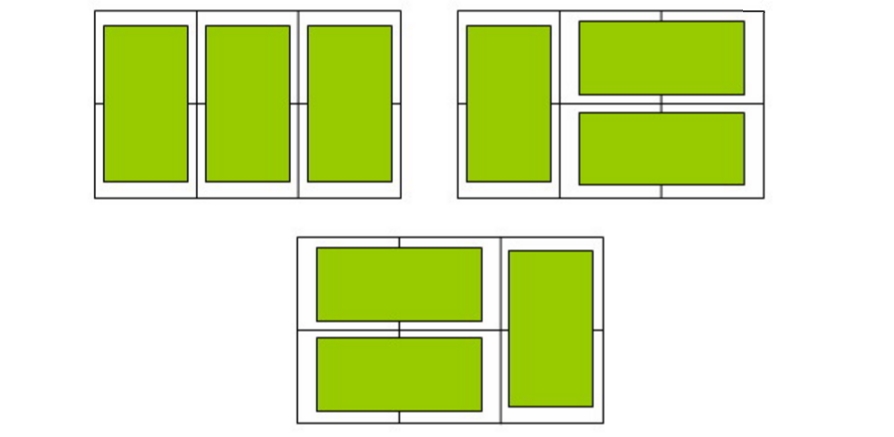
Input
输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是2*n (0< n<=50)。
Output
对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。
Sample Input
1
3
2
Sample Output
1
3
2
参考程序
#include <stdio.h>
#define LEN 50
int main()
{
int n;
while(scanf("%lld",&n)!=EOF)
{
int i;
long long a[LEN+5];
a[1]=1,a[2]=2;
for(i=3;i<=n;i++)
{
a[i]=a[i-1]+a[i-2];
}
printf("%lld\n",a[n]);
}
return 0;
}
分析
问题的本质是斐波那契数列。①当n=1时,骨牌只能竖放,即仅1种方案;②当n=2时:考虑第一块骨牌,若竖放时,则剩余一个方格只能竖放.若横放时,则一次性占用两个方格,不再有多余的空格。所以一共2种方案。③n个方格时,第一步考虑竖放,则后面剩余的n-1个空余方格通过前面的结果得出;也可以第一步考虑横放,则后面n-2个空余方格也可以通过前面的结果得出。根据分类加法原理,将两类第一步下的方法加总,从而得到了递推关系,即得到n个方格时的情形。
【例2】
Description
在3*n的一个长方形方格中,用一个1*3的骨牌铺满方格,输入n,输出铺放方案的总数. 例如n=4时,为3*4方格,骨牌的铺放方案有3种。
Input
输入数据由多行组成,每行包含一个整数n,表示该测试实例的长方形方格的规格是3*n (0< n<=50)。
Output
对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。
Sample Input
1
2
3
4
Sample Output
1
1
2
3
参考程序
#include <stdio.h>
#define LEN 50
int main()
{
int n;
while(scanf("%lld",&n)!=EOF)
{
int i;
long long a[LEN+5];
a[1]=1,a[2]=1,a[3]=2;
for(i=4;i<=n;i++)
{
a[i]=a[i-1]+a[i-3];
}
printf("%lld\n",a[n]);
}
return 0;
}
分析
与例1相同。①当n=1时,骨牌只能竖放,即仅1种方案;②当n=2时:无法横放,两块骨牌都只能竖放,即仅1种方案;③当n=3时:考虑第一块骨牌,若竖放时,则剩余两个方格也只能竖放,1种方案。若第一块骨牌横放时,则一次性占用3个方格,不再有多余的空格,剩余两块也都横放,1种方案。所以一共2种方案。④n个方格时,第一步考虑竖放,则后面剩余的n-1个空余方格通过前面的结果得出;也可以第一步考虑横放,则后面n-3个空余方格也可以通过前面的结果得出。根据分类加法原理,将两类第一步下的方案加总,从而得到了递推关系,即n个方格时的情形。
【例3】
Description
请在1*n的一个长方形方格中,任选1*1、1*2和1*3的骨牌铺满方格, 输入n,输出铺放方案的总数. 例如n=3时,为1*3的方格,骨牌的铺放方案有4种
Input
多组输入,输入到EOF结束,每行包含一个整数n,表示该测试实例的长方形方格的规格是1*n (0< n<=30)。
Output
对于每个测试实例,请输出铺放方案的总数,每个实例的输出占一行。
Sample Input
1
2
3
4
Sample Output
1
2
4
7
参考程序
#include <stdio.h>
#define LEN 50
int main()
{
int n;
while(scanf("%lld",&n)!=EOF)
{
int i;
long long a[LEN+5];
a[1]=1,a[2]=2,a[3]=4;
for(i=4;i<=n;i++)
{
a[i]=a[i-1]+a[i-2]+a[i-3];
}
printf("%lld\n",a[n]);
}
return 0;
}
分析
本题与前两例略有不同,但思路仍是斐波那契数列。①当n=1时:只能选一个1*1规格的骨牌填入,即仅1种方案;②当n=2时:可以填入两个1*1规格的骨牌,也可以填入一个1*2规格的骨牌,即2种方案;③当n=3时:第一步可以填入一个1*1规格的骨牌,然后剩余两个空余方格按n=2的情形计算,2种方案。第一步也可以一次性填入一个1*2规格的骨牌,然后剩余1个空余方格按n=1的情形计算,1种方案。还可以一次性填入一个1*3规格的骨牌,再没有空余的方格,1种方案。所以一共4种方案;④其他n个方格时:第一步可以填入1个1*1规格的骨牌,然后剩余n-1个方格根据之前的结果得出。第一步也可以填入一个1*2规格的骨牌,然后剩余n-2个根据之前的结果得出。第一步还可以填入一个1*3规格的骨牌,然后剩余n-3个空余方格根据之前的结果得出。根据分类加法原理,将三类第一步下的方法加总,从而得出递推关系,即得到n个方格的情形。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: