21、数据结构与算法实战：子集和问题-程序员快看-教程，程序员编程资料站

Description
子集和问题的一个实例为〈S,t〉。其中，S={ x1 ， x2 ，…，xn }是一个正整数的集合，c是一个正整数。子集和问题判定是否存在S的一个子集S1，使得：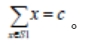
试设计一个解子集和问题的回溯法。对于给定的正整数的集合S={ x1 ， x2 ，…，xn }和正整数c，计算S 的一个子集S1，使得：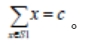
Input
输入数据的第1 行有2 个正整数n 和c（n≤10000，c≤10000000），n 表示S 的大小，c是子集和的目标值。接下来的1 行中，有n个正整数，表示集合S中的元素。

Output
将子集和问题的解输出。当问题无解时，输出“No Solution!”。

Sample Input
510
226 5 4

Sample Output
226

参考程序

#include <stdio.h>
#include <stdlib.h>
#define LEN 10000

int Sum,PrimarySet[LEN+5],NumberAmount;
int SolutionCount=0,SolutionTag[LEN+5];

void Output()
{
   
     
	if(SolutionCount==0)
	{
   
     
		printf("No Solution!\n");
	}
	else if(SolutionCount==1)
	{
   
     
		int SubSet[NumberAmount+5],ElementCnt=0,i;
		for(i=1;i<=NumberAmount;i++)
		{
   
     
			if(SolutionTag[i])
			{
   
     
				SubSet[ElementCnt++]=PrimarySet[i];
			}
		}
		for(i=0;i<ElementCnt-1;i++)
		{
   
     
			printf("%d ",SubSet[i]);
		}
		printf("%d\n",SubSet[i]);
	}
}

void Search(int i,int TW,int RW)
{
   
     
	if(i>NumberAmount)
	{
   
     
		if(TW==Sum)
		{
   
     
			SolutionCount++;
		}
		Output();
		exit(0);
	}
	else
	{
   
     
		if(TW+PrimarySet[i]<=Sum)
		{
   
     
			SolutionTag[i]=1;
			Search(i+1,TW+PrimarySet[i],RW-PrimarySet[i]);
		}
		if(TW+RW-PrimarySet[i]>=Sum)
		{
   
     
			SolutionTag[i]=0;
			Search(i+1,TW,RW-PrimarySet[i]);
		}
	}
}

int main()
{
   
     
	scanf("%d%d",&NumberAmount,&Sum);
	int RW=0,i;
	for(i=1;i<=NumberAmount;i++)
	{
   
     
		scanf("%d",&PrimarySet[i]);
		RW+=PrimarySet[i];
	}
	Search(1,0,RW);
	return 0;
}

分析：
当考察PrimarySet[i]是否加入子集时记TW为当前已选数据之和，RW为当前未选数据（包括PrimarySet[i]）之和。有如下两种动作：①若TW+PrimarySet[i]<=Sum，则将PrimarySet[i]加入子集，置SolutionTag为1，递归调用函数Search(i+1,TW+PrimarySet[i],RW-PrimarySet[i])，考察第i+1个数是否加入子集；②若TW+PrimarySet[i]>Sum说明当前加入PrimarySet[i]将超载，所以一定不能加入。考虑剩下的元素，若TW+RW-PrimarySet[i]<Sum，说明在不选择PrimarySet[i]的情况下，即便将剩余的所有数都选上，都达不到Sum，因此只有TW+RW-PrimarySet[i]>=Sum，再递归调用函数Search(i+1,TW,RW-PrimarySet[i])。当检查完所有的数，即i>NumberAmount时，若TW=Sum，说明解存在，则先统计这一组解，再输出；若不满足TW=Sum，说明解不存在，则无需统计，直接输出。具体输出情况由Output()实现。