Description
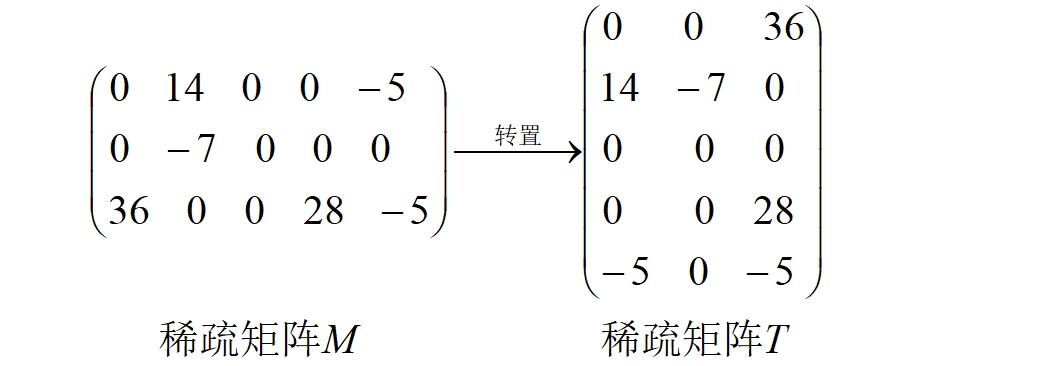
转置运算是一种最简单的矩阵运算,对于一个m*n的矩阵M( 1 = < m < = 10000,1 = < n < = 10000 ),它的转置矩阵T是一个n*m的矩阵,且T( i , j )=M( j , i )。显然,一个稀疏矩阵的转置仍然是稀疏矩阵。你的任务是对给定一个m*n的稀疏矩阵( m , n < = 10000 ),求该矩阵的转置矩阵并输出。矩阵M和转置后的矩阵T如下图示例所示。
Input
连续输入多组数据,每组数据的第一行是三个整数mu, nu, tu(tu <= 50),分别表示稀疏矩阵的行数、列数和矩阵中非零元素的个数,随后tu行输入稀疏矩阵的非零元素所在的行、列值和非零元素的值,同一行数据之间用空格间隔。(矩阵以行序为主序)
Output
输出转置后的稀疏矩阵的三元组顺序表表示。
Sample Input

Sample Output

参考程序
#include <stdio.h>
#define TABLE_LEN 50//稀疏矩阵中非零元素的个数
#define MAX_LEN 10000//稀疏矩阵行、列最大长度
struct Matrix
{
int M_Row;//行号
int M_Column;//列号
int value;//值
};
struct Matrix M[TABLE_LEN+5],T[TABLE_LEN+5];
struct Information//统计表
{
int ColumnNum;//列号
int ElementAmount;//非零元素的个数
int FirstLocation;//该列首非零元素映射到转置矩阵的行号
};
struct Information Info[MAX_LEN+5];
void Input(int RowAmount,int ColAmount,int ValueAmount)
{
int i;
M[0].M_Row=RowAmount;
M[0].M_Column=ColAmount;
M[0].value=ValueAmount;//第0行表项存储矩阵的信息:行数、列数、非零元素个数
for(i=1;i<=ValueAmount;i++)
{
Info[i].ElementAmount=0;
}//每录入一组数据之前,都需要预先将统计表的表项清零
for(i=1;i<=ValueAmount;i++)
{
scanf("%d%d%d",&M[i].M_Row,&M[i].M_Column,&M[i].value);
Info[ M[i].M_Column ].ElementAmount++;
}
Info[1].FirstLocation=1;
for(i=2;i<=ColAmount;i++)
{
Info[i].FirstLocation=Info[i-1].FirstLocation+Info[i-1].ElementAmount;
}
}
void GetTranspose(int RowAmount,int ColAmount,int ValueAmount)
{
int j;
T[0].M_Column=RowAmount;
T[0].M_Row=ColAmount;
T[0].value=ValueAmount;
for(j=1;j<=ValueAmount;j++)
{
T[ Info[ M[j].M_Column ].FirstLocation ].value=M[j].value;
T[ Info[ M[j].M_Column ].FirstLocation ].M_Row=M[j].M_Column;
T[ Info[ M[j].M_Column ].FirstLocation ].M_Column=M[j].M_Row;
Info[ M[j].M_Column ].FirstLocation+=1;
}
}
void OutputMatrix(struct Matrix a[])
{
int i;
for(i=1;i<=a[0].value;i++)
{
printf("%d %d %d\n",a[i].M_Row,a[i].M_Column,a[i].value);
}
}
int main()
{
int RowAmount,ColAmount,ValueAmount;
while(scanf("%d%d%d",&RowAmount,&ColAmount,&ValueAmount)!=EOF)
{
Input(RowAmount,ColAmount,ValueAmount);
GetTranspose(RowAmount,ColAmount,ValueAmount);
OutputMatrix(T);
}
return 0;
}
分析
本题数据结构较复杂,但均为结构体数组,将结构体数组看成一章二维表,每个结点作为一个表项即可容易理解。下面解释快速转置的步骤:
1、 初始化:稀疏矩阵用三元组表示,约定矩阵的行和列均从1开始以样例输入为例建立M矩阵的三元组表:;

2、 完成统计表:其中ColumnNum就是位置下标,无需自己设置;ElementAmount的计算在输入的同时通过累加递增完成(初始值为0);第1列的FirstLocation为1,后面每一列的FirstLocation=前一列的FirstLocation+前一列的ElementAmount;

3、 完善转置矩阵T同样矩阵T用三元组表示;
①首先第0行用来存储矩阵信息,M_Row和M_Column分别为M矩阵的M_Column和M_Row,value不变。
②从序号为1的表项开始扫描M矩阵的表格,逐一取出M_Column,以此定位到Information的M_Column列,即Information[M_Column],此表项的FirstLocation表示要将数据复制到T矩阵表格的第FirstLocation行,复制时按照转置的规则进行。复制两项的结果如下图所示:
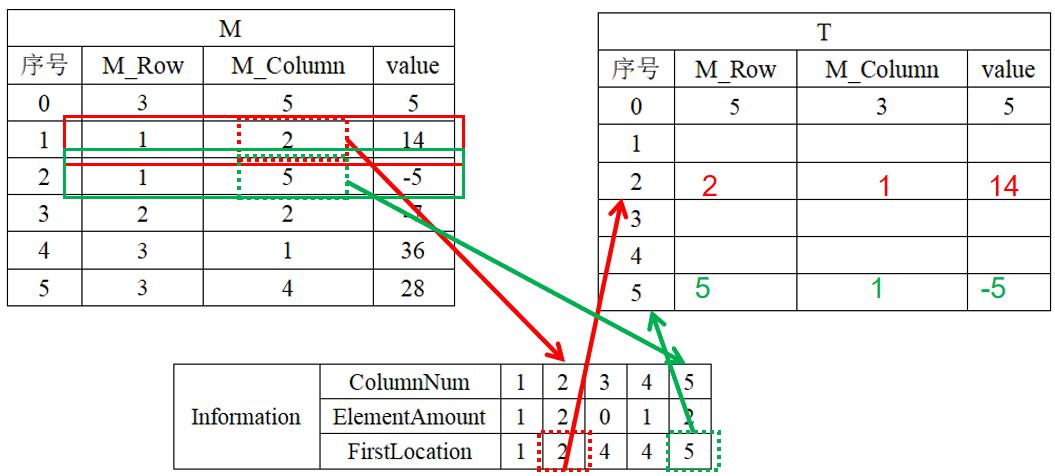
T中表项更新一条后,回到Information表,将刚才使用过的FirstLocation项加1.按照同样的方法利用循环进行操作,最后可矩阵T的表格补充完整。如下所示:

注意:每输入一组数据,都要对Information表预先清零,因为涉及统计个数的操作。在多组输入的情况下,如果没有清零,那么新的一组在统计时,因加一操作是基于上一组的结果的,会造成统计错误。(如果只输入一组,则无需清零,因为结构体定义完成后,数据变量初值为0)
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: