递归概念
简单来说就是自己调自己
递归解决的问题
数学问题:8皇后问题,迷宫问题
用到递归的算法:快速排序、归并排序、二分查找、分治算法
递归注意事项
递归一定要向退出条件逼近、否者出现无限递归、导致栈溢出异常:StackOverflowError
递归经典案例
迷宫问题
问题描述
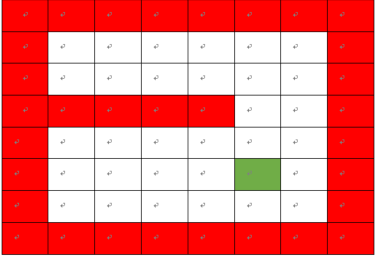
如图一个8X8的表格中,红色的代表墙,绿色的代表要到达的终点,让小球从指定地点到达绿色的位置。
实现思路
1、 构造一个二维数组;
2、 红色的用1填充、白色的用0填充、走过的路用2填充、走不通的死路用3填充;
3、 使用递归,遇到1或者3的路通过调整方向来进行递归;
代码实现
public class MiGong {
public static void main(String[] args) {
//构造迷宫
int[][] map = new int[8][8];
for (int i = 0; i < 8; i++) {
map[0][i] = 1;
map[7][i] = 1;
}
for (int i = 0; i < 8; i++) {
map[i][0] = 1;
map[i][7] = 1;
}
map[3][1] = 1;
map[3][2] = 1;
map[3][3] = 1;
map[3][4] = 1;
// 输出地图
System.out.println("地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 8; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
//使用递归回溯给小球找路
setWay(map, 1, 1);
//输出新的地图, 小球走过,并标识过的递归
System.out.println("小球走过,并标识过的 地图的情况");
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 7; j++) {
System.out.print(map[i][j] + " ");
}
System.out.println();
}
}
//使用递归回溯来给小球找路
//说明
//1. map 表示地图
//2. i,j 表示从地图的哪个位置开始出发 (1,1)
//3. 如果小球能到 map[6][5] 位置,则说明通路找到.
//4. 约定: 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙 ; 2 表示通路可以走 ; 3 表示该点已经走过,但是走不通
//5. 在走迷宫时,需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通,再回溯
/**
* @param map 表示地图
* @param i 从哪个位置开始找
* @param j
* @return 如果找到通路,就返回true, 否则返回false
*/
public static boolean setWay(int[][] map, int i, int j) {
if (map[5][5] == 2) {
// 通路已经找到ok
return true;
} else {
if (map[i][j] == 0) {
//如果当前这个点还没有走过
//按照策略 下->右->上->左 走
map[i][j] = 2; // 假定该点是可以走通.
if (setWay(map, i + 1, j)) {
//向下走
return true;
} else if (setWay(map, i, j + 1)) {
//向右走
return true;
} else if (setWay(map, i - 1, j)) {
//向上
return true;
} else if (setWay(map, i, j - 1)) {
// 向左走
return true;
} else {
//说明该点是走不通,是死路
map[i][j] = 3;
return false;
}
} else {
// 如果map[i][j] != 0 , 可能是 1, 2, 3
return false;
}
}
}
}
8皇后问题
问题描述

实现思路
1、 创建一个长度为8一维数组,角标代表第几行,角标对应的值代表这个皇后放在这一行的第几列,比如array[1]=1,代表放在第二行的第二列位置;
2、 第一个皇后放在第一列,;
3、 第二个先放第二行第一列,判断是否冲突,冲突的话放第二列,第三列直到不冲突为止;
4、 继续第三个、第四个…同样都是先放在第三行第一列、判断是否冲突,冲突的话放第二列,第三列直到不冲突为止;
5、 当得到一个正确解时,会回到上一行,继续调整列,一直得到第一个皇后第一列所有正确的解答;
6、 继续第一个皇后第二列,然后继续重复3,4,5步骤;
代码实现
public class Queue8 {
int max = 8;
int[] array = new int[max];
static int count = 0;
static int judgeCount = 0;
public static void main(String[] args) {
Queue8 queue8 = new Queue8();
queue8.check(0);
System.out.printf("一共有%d解法", count);
System.out.printf("一共判断冲突的次数%d次", judgeCount); // 1.5w
}
private void check(int n) {
if(n == max) {
//n = 8 , 其实8个皇后就既然放好
print();
return;
}
//依次放入皇后,并判断是否冲突
for(int i = 0; i < max; i++) {
array[n] = i;//先把当前这个皇后 n , 放到该行的第1列
//判断当放置第n个皇后到i列时,是否冲突
if(judge(n)) {
// 不冲突
check(n+1);//接着放n+1个皇后,即开始递归
}
//如果冲突,就继续执行 array[n] = i; 即将第n个皇后,放置在本行得 后移的一个位置
}
}
/**
*
* @param n 表示第n个皇后
* @return
*/
private boolean judge(int n) {
//查看当我们放置第n个皇后, 就去检测该皇后是否和之前已经摆放的所有的皇后冲突,有一个冲突就返回false
judgeCount++;
for(int i = 0; i < n; i++) {
// 说明
//1. array[i] == array[n] 表示判断 第n个皇后是否和前面的n-1个皇后在同一列
//2. Math.abs(n-i) == Math.abs(array[n] - array[i]) 表示判断第n个皇后是否和第i皇后是否在同一斜线
// n = 1 放置第 2列 1 n = 1 array[1] = 1
// Math.abs(1-0) == 1 Math.abs(array[n] - array[i]) = Math.abs(1-0) = 1
//3. 判断是否在同一行, 没有必要,n 每次都在递增
if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]) ) {
return false;
}
}
return true;
}
//写一个方法,可以将皇后摆放的位置输出
private void print() {
count++;
for (int i = 0; i < array.length; i++) {
System.out.print(array[i] + " ");
}
System.out.println();
}
}
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: