摘要
跳表可以降低有序链表的添加、删除和搜索的平均时间复杂度。跳表的应用场景也是比较多,比如在 Redis 中使用。它的实现逻辑也是值得去学习的。
一个有序链表的搜索、添加和删除的平均时间复杂度为 O(n)。那么,是否可以利用二分搜索法优化有序链表,使得有序链表的搜索、添加和删除的平均时间复杂度降低为 O(logn)?
我们知道,数组是可以高效的随机访问的,因为数组是存在索引的。但是链表不具备索引,所以不能像有序数组那样直接使用二分搜优化。那么有什么其他方法可以让有序数组的搜索、添加和删除的平均时间复杂度为 O(logn) 呢?
答案是一定存在的,那就是跳表!!!
什么是跳表?
跳表也被称为跳跃表,或者跳跃列表,就是在有序链表的基础上增加了“跳跃”的功能。它是由 William Pugh 在 1990 年发布的,设计的初衷是为了取代平衡树(比如红黑树)。
著名的Key-Value 数据库,比如 Redis 和 LevelDB。Redis 中的 SortedSet,LevelDB 中的 MemTable 都用到了跳表。
跳表相对于平衡树,跳表的实现和维护会更加简单。跳表的搜索、删除和添加的平均时间复杂度是 O(logn),如下图(图片来自网络)。
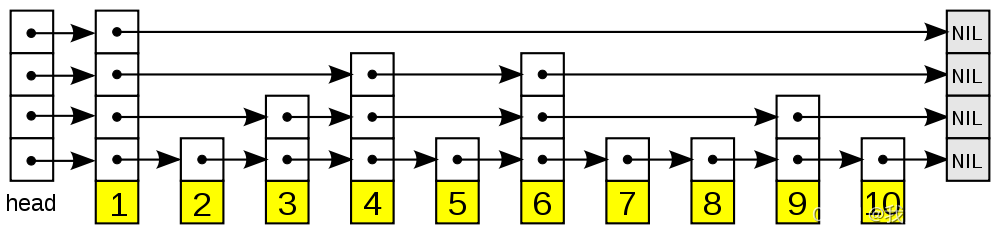
搜索
在跳表中搜索时,按照以下步骤进行:
1、 从顶层链表的首元素开始,从左到右搜索,直至找到一个大于或等于目标的元素,或者到达当前层链表的尾部;
2、 如果该元素等于目标元素,则表明该元素已被找到;
3、 如果该元素大于目标元素或者已到达链表的尾部,则退回到当前层的前一个元素,然后转入下一层进行搜索;
添加和删除
跳表中添加元素时,随机确定新添加元素的层数。删除元素时,整个跳表的层数也可能会降低。
层数
跳表是按照层构建的,底层是一个普通的有序链表,高层相当于是低层的“快速通道”。
假设在第 i 层出现的元素 x,在第 i+1 层出现 x 的固定概率为 p,那么,产出越高的层数,概率就越低了,比如:
- 元素层数恰好等于 1 的概率为 1-p;
- 元素层数大于等于 2 的概率为 p,而元素层数恰好等于 2 的概率为 p*(1-p);
- 元素层数大于等于 3 的概率为 p^2,而元素层数恰好等于 3 的概率为 p^2 * (1-p);
- 元素层数大于等于 4 的概率为 p^3,而元素层数恰好等于 4 的概率为 p^3 * (1-p);
- …
以此类推,一个元素的平均层数是 1 / (1 - p)。通常 p 的值设置为 1/2 或者 1/4,所以每个元素所包含的平均指针数量是 2 或者 1.33。
实现代码
先创建一个类,在类中定义一些属性,并实现一些简单的函数:
public class SkipList<K, V> {
// 最大层数
private static final int MAX_LEVEL = 32;
// 概率值
private static final double p = 0.5;
// 元素数量
private int size;
// 比较函数
private Comparator<K> comparator;
// 有效层数
private int level;
// 不存放任何 K-V
private Node<K, V> first;
public SkipList(Comparator<K> comparator) {
this.comparator = comparator;
first = new Node<>(null, null, MAX_LEVEL);
first.nexts = new Node[MAX_LEVEL];
}
public SkipList() {
this(null);
}
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
}
comparator 属性定义时需要引入 java.util.Comparator 系统工具类。
在SkipList 类的构造函数中,可以看到 Node 类的创建需要传入 3 个参数,其中一个是传递层数,因为 Node 中需要定义一个数组来存放指向不同层的指针:
private static class Node<K, V> {
K key;
V value;
Node<K, V>[] nexts;
public Node(K key, V value, int level) {
super();
this.key = key;
this.value = value;
this.nexts = new Node[level];
}
}
添加元素
接下来实现添加元素函数,在实现过程中要这几步走:
1、 从顶层开始,遍历每一层,找到要添加元素的所有前驱节点,如果出现添加的元素和跳表中的元素相同,那么就替换它,结束;
2、 对新添加的元素创建一个新的节点,随机一个层数,然后遍历新的层数,将新的节点添加进去;
3、 size加一,重新确定跳表的层高;
public V put(K key, V value) {
keyCheck(key);
Node<K, V> node = first;
Node<K, V>[] prevs = new Node[level];
for (int i = level - 1; i >= 0; i--) {
int cmp = -1;
while (node.nexts[i] != null && (cmp = compare(key, node.nexts[i].key)) > 0) {
node = node.nexts[i];
}
if (cmp == 0) {
// 节点存在
V oldV = node.nexts[i].value;
node.nexts[i].value = value;
return oldV;
}
prevs[i] = node;
}
// 新节点的层数
int newLevel = randomLevel();
// 添加新节点
Node<K, V> newNode = new Node<>(key, value, newLevel);
// 设置前驱和后继
for (int i = 0; i < newLevel; i++) {
if (i >= level) {
first.nexts[i] = newNode;
} else {
newNode.nexts[i] = prevs[i].nexts[i];
prevs[i].nexts[i] = newNode;
}
}
// 节点数量增加
size++;
// 计算跳表的最终层数
level = Math.max(level, newLevel);
return null;
}
随机层数的函数需要 p 和 MAX_LEVEL 一起来确定:
private int randomLevel() {
int level = 1;
while (Math.random() < p && level < MAX_LEVEL) {
level ++;
}
return level;
}
搜索元素
搜索元素就简单很多了,就是一层层的遍历,每一层都从头遍历到尾部,直至找到元素或者全部遍历完:
public V get(K key) {
keyCheck(key);
Node<K, V> node = first;
for (int i = level-1; i >= 0; i--) {
int cmp = -1;
while (node.nexts[i] != null && (cmp = compare(key, node.nexts[i].key)) > 0) {
node = node.nexts[i];
}
if (cmp == 0) return node.nexts[i].value;
}
return null;
}
删除元素
删除元素和添加元素的第一步比较相似,需要多留意不同的地方:
1、 从高层到低层,从头到尾,依次遍历,获取要删除元素的前驱节点,并有个标识,来确定是否存在要删除的元素;
2、 删除节点,也就是要删除的节点的前驱节点指向要删除节点的后继,层与层之间要对应好;
3、 更新层数,如果first节点直接指向null,那么就可以删除该层了;
public V remove(K key) {
keyCheck(key);
Node<K, V> node = first;
Node<K, V>[] prevs = new Node[level];
boolean exist = false;
for (int i = level-1; i >= 0; i--) {
int cmp = -1;
while (node.nexts[i] != null && (cmp = compare(key, node.nexts[i].key)) > 0) {
node = node.nexts[i];
}
prevs[i] = node;
if (cmp == 0) exist = true;
}
if (!exist) return null;
// 需要被删除的节点
Node<K, V> removeNode = node.nexts[0];
// 设置前驱和后继 ???
for (int i = 0; i < removeNode.nexts.length; i++) {
prevs[i].nexts[i] = removeNode.nexts[i];
}
// 更新跳表的层数
int newLevel = level;
while (--newLevel >= 0 && first.nexts[newLevel] == null) {
level = newLevel;
}
// 数量减1
size--;
return removeNode.value;
}
为什么
Node<K, V> removeNode = node.nexts[0];就是要删除的节点?因为跳表的最底层就是一个包含所以节点的有序链表,添加元素也是从底层开始的,node 已经是要删除节点的前驱节点了, nexts[0] 就是最底层的节点,必然指向要删除的节点。
总结
- 跳表可以让添加、删除和搜索的平均时间复杂度降低为 O(logn);
- 跳表是二分法的思维实现;
- 跳表更改前驱和后继是添加和删除函数的重点。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: