10、数据结构与算法进阶：生成树、kruskal算法-程序员快看-教程，程序员编程资料站

摘要

Kruskal 是求最小生成树的算法，本质就是依次将权值小的边不断并入最小生成树中。这期间可能会形成环，这里使用并查集的数据结构来避免形成环，这个点是非常巧妙的。

上期详细介绍了生成树的概念，即图中边的数量是顶点数量减1，在一些计算多点相连的成本计算场景中使用最小生成树是一个很好的选择。随后介绍 Prim 算法获得最小生成树。Prim 算法就是通过切分将权值最小的顶点划分到同一个集合中，下面将要介绍另外一个求最小生成树的算法，即 Kruskal 算法。

Kruskal 算法比较直接，即将图中的边按照权值由小到大依次加入生成树中，直到边的数量是顶点数量减一为止，也可以是顶点的数量等于原来图中顶点的数量。

如下图所示，左侧图中的到的最小生成树就是右侧图所示：

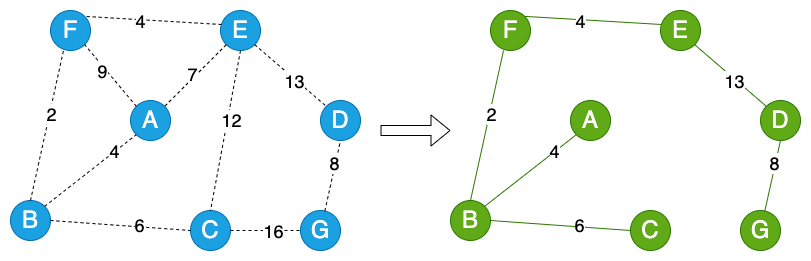
上图中获取最小生成树，用 Kruskal 算法的流程如下图（从左到右，从上到下）：

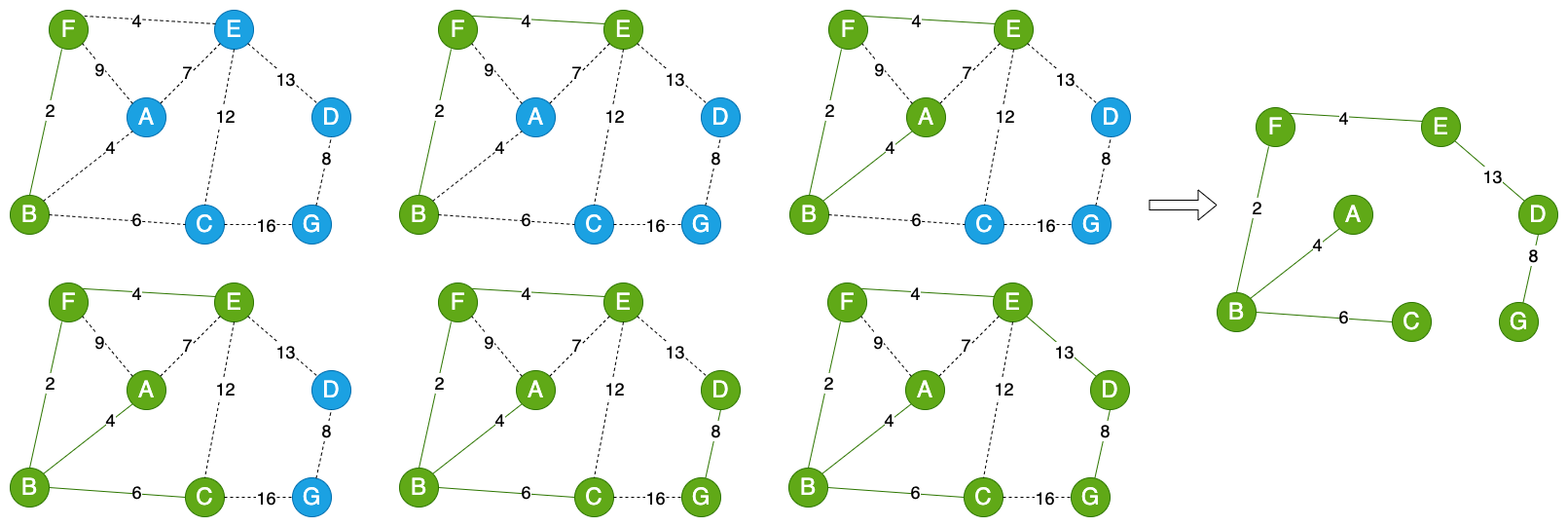
由图中可以看出，依次找到权值最小的边，这里面要特别注意，如果加入某一个边，会形成环，则不能加入该边，比如考虑是否加入权值是 12 的边。在刚加入第一条或者第二条边时，不会有环，当添加第三条边时就有可能产生环，所以如果判断是否形成环可以从添加第三条边时做判断。

按照惯例，先上代码：

Set<EdgeInfo<V, E>> kruskal() {
   
     
    int edgeSize = vertices.size() -1;
    if (edgeSize == -1) return null;

    Set<EdgeInfo<V, E>> edgeInfos = new HashSet<>();
    MinHeap<Edge<V, E>> heap = new MinHeap<>(edges, edgeComparator);

    UnionFind<Vertex<V, E>> uf = new UnionFind<>();
    vertices.forEach((V v, Vertex<V, E> vertex) -> {
   
     
        uf.makeSet(vertex);
    });
    int verticesSize = vertices.size();
    while (!heap.isEmpty() && edgeInfos.size() < verticesSize-1) {
   
     
        Edge<V, E> edge = heap.remove();
        if (uf.isSame(edge.from, edge.to)) continue;
        edgeInfos.add(edge.info());
        uf.union(edge.from, edge.to);
    }

    return edgeInfos;
}

kruskal 函数返回的是 EdgeInfo 类型的集合，Edgeinfo 主要存放的是起始顶点、结束顶点和权值：

public static class EdgeInfo<V, E> {
   
     
    private V from;
    private V to;
    private E weight;

    public EdgeInfo(V from, V to, E weight) {
   
     
        this.from = from;
        this.to = to;
        this.weight = weight;
    }

kruskal 函数的前两行代码，是获取生成最小树时边的数量，并直接通过数量判断图是否存在。

int edgeSize = vertices.size() -1;
if (edgeSize == -1) return null;

接下来创建 edgeInfos存放边信息，作为函数的返回数据。之后使用小顶堆把所有边放进去（小顶堆，是保证权值最小的边在第一的位置），对小顶堆感兴趣可以看《数据结构与算法-基础（十九）堆》文章。

Set<EdgeInfo<V, E>> edgeInfos = new HashSet<>();
MinHeap<Edge<V, E>> heap = new MinHeap<>(edges, edgeComparator);

然后依次从 heap 中取出边，添加到 edgeInfos 中，直到 heap 没有边或者边的数量等于顶点减一时结束。这个逻辑和 Prim 算法一致。

但是最小生成树是不能出现环的，为了避免这种情况出现，方法中使用到了并查集的方式（对并查集感兴趣的可以看《数据结构与算法-进阶（一）并查集）。

那么并查集是如何判断是否存在环呢？首先从并查集的本质出发，它就是将两个不同集合合并到同一个集合，集合中的元素最终指向同一个根元素，并切可以查看某元素所在的集合和另外一个集合是否在同一个集合中。

这里是将并入最小生成树的顶点也放到并查集中，在后面添加边时，通过并查集的方法判断边的两个顶点是否已经属于同一个集合中（在并查集中），如果存在，那么再加入这个边就形成了环。

if (uf.isSame(edge.from, edge.to)) continue;
edgeInfos.add(edge.info());
uf.union(edge.from, edge.to);

所以在代码中就是先判断边的两个顶点是否是属于同一个集合，不属于再添加到 edgeInfos 中，并将这两个顶点合并到一个集合中，再回到循环的开始位置继续进行。

在循环开始前，有如下代码，目的是将顶点都先保存在并查集中，在判断或者添加顶点时，用做判断这个顶点是否属于图中的顶点，如果不属于就不做判断或者合并等操作，避免不必要的处理：

UnionFind<Vertex<V, E>> uf = new UnionFind<>();
vertices.forEach((V v, Vertex<V, E> vertex) -> {
   
     
    uf.makeSet(vertex);
});

总结

Kruskal 是求最小生成树的算法，就是依次加入权值小的边；
其中用到小顶堆，就是方便不断获取权值小的边；
为了避免边形成环，这里使用并查集的数据结构，就是将边相连的顶点放在同一个集合中，通过判断两个顶点是否属于同一个集合来确定是否会形成环。这个点很巧妙。