数据结构与算法-进阶(三)图
摘要
数据结构中第三大分类就是图结构。简单地理解,图就是由顶点和边组成的。根据顶点的分布和边的连接这两种情况,可以分成不同的类型。接下来将介绍图以及它的大致分类。
回顾之前的数据结构,大致可以线性结构和树形结构。线性结构比如数组、链表、栈、队列、哈希表;树形结构比如二叉树、B树、堆、Trie、哈夫曼树、并查集。现在要正式接触第三种数据结构 — 图。
图(Graph)是由顶点(vertex)和边(edge)组成,通常的表达式是 G = (V, E)。看字母大致可以理解到,G 表示一个图,V 表示它的顶点集合,E 表示它的边集合,它们的特性如下:
- 一个图中的顶点必须有,可以有很多,但一定是有限的;
- 任意两个顶点可以用线来连接,表示两个顶点的关系,一个图中可以没有一个连线。
如下所示,有三个图:
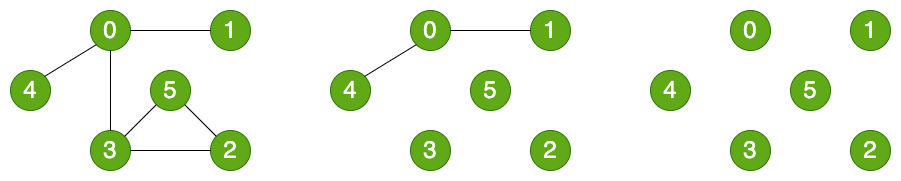
图的应用场景非常广泛,比如开车时开启的导航,玩游戏时看的地图,微信应用中的社交好友关系等。这些都是使用图来描述的。
图的分类
有向图
有向图是连接两个顶点的边有明确的方向(或指向):
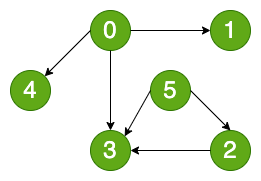
有向图中,有另外一个分类,就是无环和有环,比如从任意顶点出发无法经过若干条边回到该顶点,那么它就是一个有向无环图(比如上图)。反之就是有向有环图,比如下图所示:
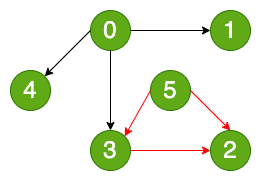
无向图
看过有向图之后,再看无向图就非常容易理解,无向图就是没有方向的图,比如下图:
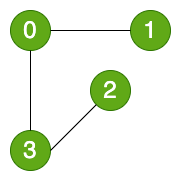
无向图也可以用有向图来表示,比如上图中的无向图用有向图表示,可以如下图所示:
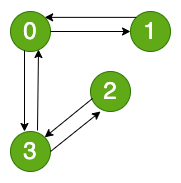
混合图
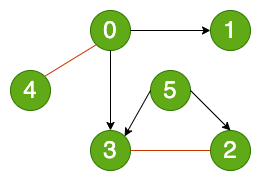
混合图边可能是无向的,也可能是有向的,比如下图,0到4和3到5的连线是无向的,其他的连线是有向的:
多重图
在介绍其他图之间,需要先了解一下平行边,下面有两种情况的平行边:
- 在无向图中,关联一对顶点的无向边如果多于1条,则称这些边是平行边;
- 在有向图中,关联的一对顶点的有向边如果多于1条,并且它们的方向相同,则称这些边为平行边。
还有个概念,就是自环,一个顶点的边两头都指向自己。
那么有平行边或者有自环的图就是多重图。与之相反的是简单图,即没有平行边也没有自环的图就是简单图,之后文章讨论的基本都是简单图。
总结
- 图是由顶点和边组成的;
- 一个图可以没有边,但是不能没有顶点
- 根据连接顶点的边是否有方向,可以分为有向图和无向图;
- 根据是否有平行边,可以分为多重图和简单图。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: