15、数据结构与算法C++：二叉排序树-程序员快看-教程，程序员编程资料站

二叉排序树

对于查找来说，自然有序数据集更方便查找。但是如果需要经常插入删除操作，有序数据集则需要更多的时间成本。有没有既方便查找也有利于插入和删除的方法呢？这里介绍一种方法——二叉排序树。
二叉排序树( Binary Sort Tree)，又称为二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树。

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
它的左、右子树也分别为二叉排序树

相关代码如下：

#include<vector>
using namespace std;
class BinSortT
{
public:
    BinSortT();
    ~BinSortT();
    friend void CreateBSTree(vector<int>t, int k, BinSortT* T, BinSortT *P);//根据一组数据创建二叉排序树
    friend bool SearchBST(BinSortT* T, int key);//查找
    friend bool InsertBST(BinSortT* T, int key);//查找不成功插入
    friend bool DeleteBST(BinSortT* T, int key);//删除数据
    friend bool Delete(BinSortT* T);//删除操作
    friend bool D(BinSortT *T, int key);
private:
    int data;
    BinSortT*lchild, *rchild;
};

#include<iostream>
#include "BinSortT.h"

using namespace std;
int main()
{
    vector<int>t;
    int n,val,k=0;
    BinSortT *T, *P;
    T = new BinSortT;
    P = T;
    cout << "输入数组元素的个数:";
    cin >> n;
    cout << "输入数组元素:" << endl;
    for (int i = 0; i < n; i++)
    {
        cin >> val;
        t.push_back(val);
    }
    CreateBSTree(t,k,T,P);
    cout << "成功生成二叉排序树,请输入要查询元素" << endl;
    cin >> val;
    if (InsertBST(T, val))cout << "查询成功，找到元素" << endl;
    else cout << "未找到,已添加" << endl;
    cout << "请输入要查询元素" << endl;
    cin >> val;
    if (SearchBST(T, val))cout << "查询成功，找到元素" << endl;
    else cout << "查询失败" << endl;
    cout << "请输入要删除元素" << endl;
    cin >> val;
    if (DeleteBST(T, val))cout << "删除成功" << endl;
    else cout << "删除失败" << endl;
    cout << "请输入要查询元素" << endl;
    cin >> val;
    if (SearchBST(T, val))cout << "查询成功，找到元素" << endl;
    else cout << "查询失败" << endl; 
    system("pause");
    return 0;
}
void CreateBSTree(vector<int>t, int k, BinSortT *T, BinSortT *P)//根据一组数据创建二叉排序树
{
    T->data = t[k++];
    while (k < t.size())
    {
        if (t[k] < P->data)
        {
            if (!P->lchild)
            {
                P->lchild = new BinSortT;
                P->lchild->data = t[k++];
                P = T;
            }
            else
            {
                P = P->lchild;
            }
        }
        else if (t[k] > P->data)
        {
            if (!P->rchild)
            {
                P->rchild = new BinSortT;
                P->rchild->data = t[k++];
                P = T;
            }
            else
            {
                P = P->rchild;
            }
        }
    }
}
bool SearchBST(BinSortT* T, int key)//查找
{
    if (!T)
        return false;
    if (key == T->data)
        return true;
    if (key < T->data)
        SearchBST(T->lchild, key);
    else
        SearchBST(T->rchild, key);
}
bool InsertBST(BinSortT* T, int key)//查找不成功插入
{
    if (!T)
    {
        T = new BinSortT;
        T->data = key;
        return false;
    }
        while (T)
        {
            if (key == T->data)return true;
            if (key < T->data)
            {
                if (!T->lchild)
                {
                    T->lchild = new BinSortT;
                    T->lchild->data = key;
                    return false;
                }
                else
                {
                    T = T->lchild;
                }
            }
            else if (key > T->data)
            {
                if (!T->rchild)
                {
                    T->rchild = new BinSortT;
                    T->rchild->data = key;
                    return false;
                }
                else
                {
                    T = T->rchild;
                }
            }

        }

}
bool DeleteBST(BinSortT* T, int key)//删除数据
{
    if (!T)return false;
    if (key == T->data)
        return Delete(T);
    else if (key < T->data)
        return DeleteBST(T->lchild, key);
    else if (key >T->data)
        return DeleteBST(T->rchild, key);
}
bool Delete(BinSortT* T)//删除操作
{
    BinSortT *q, *s;
    if (T->rchild==NULL)
    {
        q = T->lchild;
        *T = *(T->lchild);
        delete q;

    }
    else if(T->lchild == NULL)
    {
        q = T->rchild;
        *T = *(T->rchild);
        delete q;
    }
    else
    {
        s = T->lchild;
        q = T;
        while (s->rchild)
        {
            q = s;
            s = s->rchild;
        }

        T->data = s->data;
        if (q != T)
            q->rchild = s->lchild;
        else
            q->lchild = s->lchild;
        delete s;
    }
    return true;
}

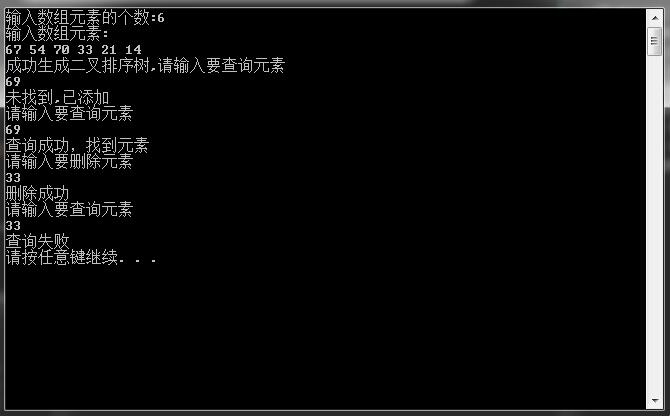
在VS上运行结果如下：