08、数据结构与算法C++：二叉树-程序员江小北

二叉树

二叉树是一种应用十分广泛的树结构。我们先来看下二叉树的定义。

二叉树( Binary Tree) 是n(n⩾0) n ( n ⩾ 0 ) 个结点的有限集合，该集合或者为空集(称为空二叉树)，或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

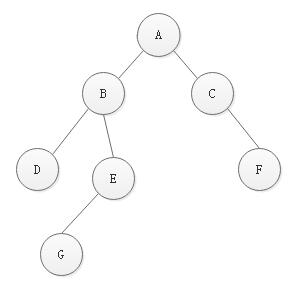
图1图 1

二叉树特点

1、每个结点最多有两棵子树；
2、左子树和右子树是有顺序的，次序不能任意颠倒；
3、即使树中某结点只有一棵子树，也要区分它是左子树还是右子树；

特殊二叉树

斜树

所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

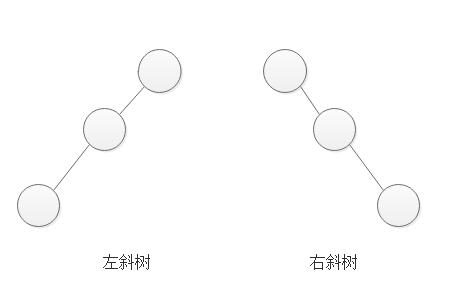
图2图 2

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

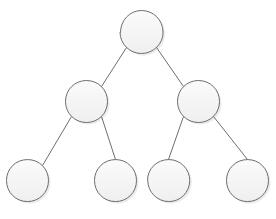
图3图 3

完全二叉树

对一棵具有n n 个结点的二叉树按层序编号，如果编号为i(1⩽i⩽n) i ( 1 ⩽ i ⩽ n ) 的结点与同样深度的满二叉树中编号为i i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

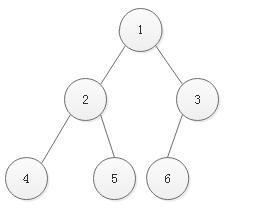
图4图 4

要注意将完全二叉树与满二叉树区分开。完全二叉树是满二叉树最深层从最右边的结点开始缺失若干个连续编号的结点。

二叉树的性质

性质 1 :在二叉树的第i i 层上至多有2i−1 2 i − 1 个结点(i⩾1) ( i ⩾ 1 ) 。

性质 2: 深度为k k 的二叉树至多有2k−1 2 k − 1 个结点(k⩾1) ( k ⩾ 1 ) 。

性质 3: 对任何一棵二叉树T T ，如果其终端结点数为n0 n 0，度为 2 的结点数为n2 n 2 ，则n0=n2+1 n 0 = n 2 + 1 。

性质 4: 具有n n 个结点的完全二叉树的深度为*log2n*+1 * log 2 ⁡ n * + 1 (*x* * x * 表示不大于x x 的最大整数)。

性质 5: 如果对一棵有n n个结点的完全二叉树(其深度为*log2n*+1 * log 2 ⁡ n * + 1 ) 的结点按层序编号(从第 1 层到第*log2n*+1 * log 2 ⁡ n * + 1 层，每层从左到右) ，对任一结点i(1⩽i⩽n) i ( 1 ⩽ i ⩽ n ) 有:

1、如果i=1i=1，则结点ii是二叉树的根，无双亲;如果i>1i>1，则其双亲是结点*i/2**i/2*；
2、如果2i>n2i>n，则结点ii无左孩子(结点ii为叶子结点);否则其左孩子是结点2i2i；
3、如果2i+1>n2i+1>n，则结点ii无右孩子;否则其右孩子是结点2i+12i+1；

二叉树遍历方法

**前序遍历:**规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。图1中树的前序遍历顺序为ABDEGCF。
**中序遍历:**规则是若树为空，则空操作返回，否则从根结点开始(注意并不是先访问根结点) ，中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。如图1中树的中序遍历顺序为DBGEACF。
**后序遍历:**规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。如图1中树的后序遍历顺序为DGEBFCA。
**层序遍历:**规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。如图1中树的层序遍历顺序为ABCDEFG。

己知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知后序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。
已知前序和后序遍历，是不能确定一棵二叉树的。

我们再来看下二叉树的代码结构：

class BTNode
{
public:
    BTNode();
    ~BTNode();
    void PreTraverseBTree();//前序遍历
    void InTraverseBTree();//中序遍历
    void PostTraverseBTree();//后序遍历
    friend void  CreateBTree(BTNode * T);//创建二叉树
private:
    char data;//数据元素
    BTNode * pLchild;//左孩子
    BTNode * pRchild ;//右孩子

};

代码的具体实现：

#include "BTNode.h"
#include<iostream>
using namespace std;
BTNode::BTNode()
{
}
BTNode::~BTNode()
{
}
void BTNode::PreTraverseBTree()
{

    if(data)cout << data << " ";
    if (pLchild!=NULL)pLchild->PreTraverseBTree();
    if (pRchild!= NULL)pRchild->PreTraverseBTree();
}
void BTNode::InTraverseBTree()
{
    if (pLchild != NULL)pLchild->InTraverseBTree();
    if (data)cout << data << " ";
    if (pRchild != NULL)pRchild->InTraverseBTree();
}
void BTNode::PostTraverseBTree()
{
    if (pLchild != NULL)pLchild->PostTraverseBTree();
    if (pRchild != NULL)pRchild->PostTraverseBTree();
    if (data)cout << data << " ";
}

二叉树的遍历是通过递归来实现的。

#include<iostream>
#include "BTNode.h"
using namespace std;
void  CreateBTree(BTNode * T);
int main()
{
    BTNode *T = new BTNode;
    CreateBTree(T);
    cout << "前序:";
    T->PreTraverseBTree();
    cout << endl;
    cout << "中序:";
    T->InTraverseBTree();
    cout << endl;
    cout << "后序:";
    T->PostTraverseBTree();
    cout << endl;
    system("pause");
    return 0;
}
void CreateBTree(BTNode * T)
{

    char ch;
    cin >>ch;
    if ('#' == ch)
    {
        T=NULL;
    }
    else{
        T->data = ch;
        T->pLchild = new BTNode;
        CreateBTree(T->pLchild);
        T->pRchild = new BTNode;
        CreateBTree(T->pRchild);
    }

}

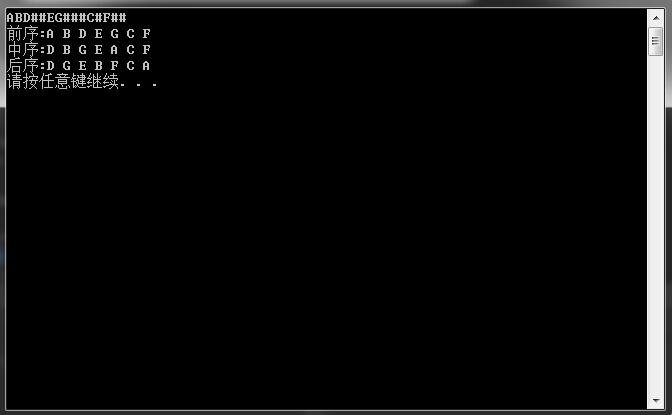
这里创建二叉树采用前序遍历来输入遇到用‘＃’表示空树，如图１中的树可以输成ABD##EG###C#F##。在VS上运行结果如下：