10、数据结构与算法C++：最小生成树-程序员快看-教程，程序员编程资料站

最小生成树

在生活中我们可能会遇到诸如多个地点架设通信网络、水管等等问题，如何设计出最小的成本的方案？

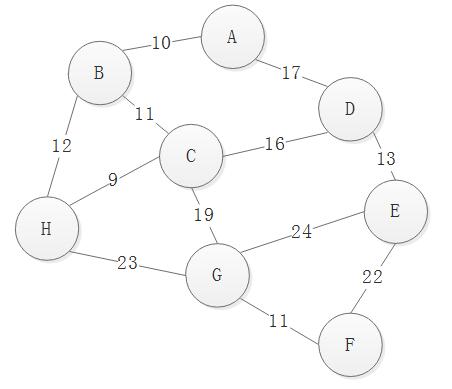
图1图 1

上图是一个带权值的图，即网结构。所谓的最小成本，就是n n 个顶点，用n−1 n − 1 条边把一个连通图连接起来，并且使得权值的和最小。像这样把构造连通网的最小代价生成树称为最小生成树( Minimun Cost Spanning Tree)。

找连通网的最小生成树，经典的有两种算法，普里姆算法和克鲁斯卡尔算法。

普里姆( Prim )算法

假设N=(P，{ E}) N = ( P ， { E } ) 是连通网，TE T E 是N N 上最小生成树中边的集合。算法从U={ u0}(u0*V) U = { u 0 } ( u 0 * V ) ， TE={ } T E = { } 开始。重复执行下述操作:在所有u*U,v*V−U u * U , v * V − U 的边(u，v)*E ( u ， v ) * E 中找一条代价最小的边(u0，v0) ( u 0 ， v 0 ) 并入集合TE T E ，同时v0 v 0 并入U U ，直至U=V U = V 为止。此时TE T E 中必有n−1 n − 1 条边，则T=(V,{ TE}) T = ( V , { T E } ) 为N N 的最小生成树。相关代码如下：

void Graph::MiniSpanTree_Prim()//Prim 算法生成最小生成树
{
    vector<int> adjvex;//保存顶点下标
    vector<int> lowcost;//保存顶点间边的权值
    int min,j,k;
    lowcost.push_back(0);
    adjvex.push_back(0);
    for (int i =1; i < numVertexes; i++)
    {
        lowcost.push_back(arc[0][i]);
        adjvex.push_back(0);
    }
    for (int i = 1; i < numVertexes; i++)
    {
        min = INFINITY;
        j = 1; k = 0;
        while (j < numVertexes)
        {
            if (lowcost[j] != 0 && lowcost[j] < min)
            {
                min = lowcost[j];
                k = j;
            }
            j++;
        }
        cout << "(" << adjvex[k] << "," << k << ")" << endl;
        lowcost[k] = 0;
        for (j = 1; j < numVertexes; j++)
        {
            if (lowcost[j] != 0 && arc[k][j] < lowcost[j])
            {
                lowcost[j] = arc[k][j];
                adjvex[j] = k;
            }
        }
    }
}

#include<iostream>
#include "Graph.h"
using namespace std;

int main()
{
    Graph G;
    G.CreateGraph();
    cout << "最小生成树：" << endl;
    G.MiniSpanTree_Prim();
    system("pause");
    return 0;
}

Graph类的相关定义可以看上一篇文（走进数据结构和算法（c++版）（9）——图）中关于邻接矩阵的代码。输入图1中的网图，在VS下运行结果如下：

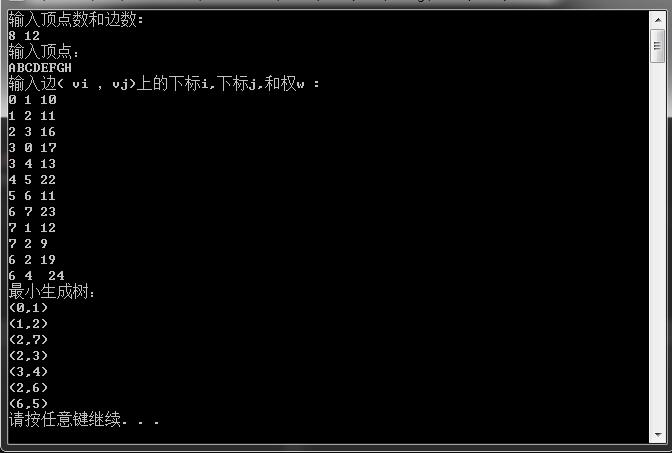
克鲁斯卡尔( Kruskal )算法

假设N=(V，{ E}) N = ( V ， { E } ) 是连通网，则令最小生成树的初始状态为只有n n 个顶点而无边的非连通图T={ V,{ }} T = { V , { } } ，图中每个顶点自成一个连通分量。在E E 中选择代价最小的边，若该边依附的顶点落在T T 中不同的连通分量上，则将此边加入到T T中，否则舍去此边而选择下一条代价最小的边。依次类推，直至T T 中所有顶点都在同一连通分量上为止。相关代码如下：

bool comp(Edge a, Edge b)//比较函数
{
    return a.weight < b.weight;
}
void Graph::MiniSpanTree_Kruskal()//Kruskal算法生成最小生成树
{
    int n, m;
    vector<Edge> edges;
    Edge e;
    vector<int> parent;
    for (int i = 1; i < numVertexes; i++)//将邻接矩阵转化到边集数组
    {
        for (int j = 0; j < i; j++)
        {
            if (arc[i][j] != 0 && arc[i][j]!= INF)
            {
                if (i < j)
                {
                    e.begin = i;
                    e.end = j;
                }
                else
                {
                    e.begin = j;
                    e.end = i;
                }
                e.weight = arc[i][j];
                edges.push_back(e);
            }
        }
    }
    sort(edges.begin(),edges.end(),comp);//边集数组排序
    for (int i = 0; i < numVertexes; i++)
        parent.push_back(0);
    for (int i = 0; i < numEdges; i++)
    {
        n = Find(parent,edges[i].begin);
        m = Find(parent, edges[i].end);
        if (n != m)
        {
            parent[n] = m;
            cout << "(" << vexs[edges[i].begin] << "," << vexs[edges[i].end] << ")" << " " << edges[i].weight << endl;
        }
    }

}
int Graph::Find(vector<int> & parent, int f)
{
    while (parent[f]>0)
        f = parent[f];
    return f;
}

#include<iostream>
#include "Graph.h"
#include<algorithm>
using namespace std;

int main()
{

    Graph G;
    G.CreateGraph();
    cout << "最小生成树：" << endl;
    G.MiniSpanTree_Kruskal();
    system("pause");
    return 0;
}

输入图1中的网图，在VS下运行结果如下：

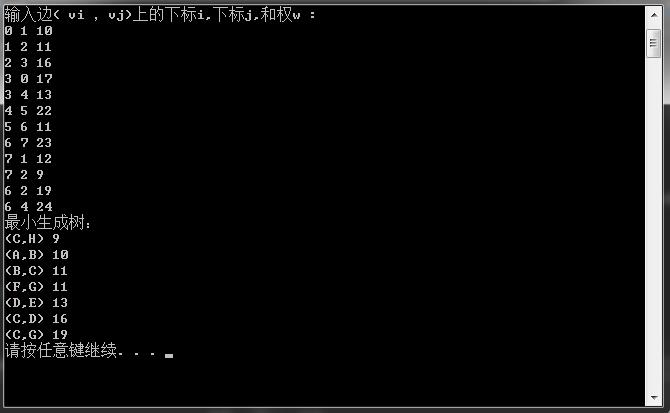
两种算法比较

克鲁斯卡尔算法主要是针对边来展开，边数少时效率会非常高，所以对于稀疏图有很大的优势i；而普里姆算法对于稠密图，即边数非常多的情况会更
好一些。