关键路径
在一个工程中可能并行多条支路,如何求出一个工程的所需最短时间?
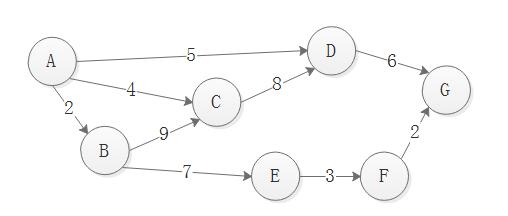
图1图 1
如上图,在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,这种有向图的边表示活动的网, 我们称之为AOE 网( Activity On EdgeNetwork)。
要想找到最短时间就必须要分析它们的拓扑关系,并且找到当中最关键的流程,这个流程的时间就是最短时间。我们先来了解下几个概念:
- 事件的最早发生时间etv e t v :即顶点Vk V k 的最早发生时间。
- 事件的最晚发生时间Itv I t v :即顶点Vk V k 的最晚发生时间。也就是每个顶点对应的事件最晚需要开始的时间,超出此时间将会延误整个工期。
- 活动的最早开工时间ete e t e :即弧ak a k 的最早发生时间。
- 活动的最晚开工时间Ite I t e :即弧ak a k 的最晚发生时间。
相关代码如下:
#include<vector>
#include<stack>
#define INFINITY 65535
using namespace std;
struct EdgeNode//边表结点
{
int adjvex;//顶点下标
int weight;//权值
EdgeNode *next;//下一个结点
};
struct VertexNode//顶点表结点
{
char vert;//顶点信息
int in = 0;//入度
EdgeNode* firstedge;//边表头指针
};
class GraphAdjList
{
public:
GraphAdjList();
~GraphAdjList();
void CreateALGraph();//构建网图
void BFSTraverse();//广度历遍算法
bool TopologicalSort();//拓扑排序
void Critica1Path();//求关键路径
private:
vector<VertexNode> adjList;
vector<bool> visited;//访问标志数组
int numVertexes, numEdges;//顶点数、边数
vector<int> etv;//事件最早开始时间
vector<int> ltv;//事件最晚开始时间
stack<int> stack0;//存储拓扑序列的栈
};
#include "GraphAdjList.h"
#include<iostream>
#include<queue>
#include<stack>
using namespace std;
GraphAdjList::GraphAdjList()
{
}
GraphAdjList::~GraphAdjList()
{
}
void GraphAdjList::CreateALGraph()//构建网图
{
int i, j, w;
cout << "输入顶点数和边数:" << endl;
cin >> numVertexes >> numEdges;
cout << "输入顶点:" << endl;
VertexNode vert;
for (int k = 0; k < numVertexes; k++)
{
cin >> vert.vert;
vert.firstedge = NULL;
adjList.push_back(vert);
}
cout << "输入边( vi ,vj)上的下标i,下标j,和权w :" << endl;
for (int k = 0; k < numEdges; k++)
{
cin >> i >> j >> w;
EdgeNode *p = new EdgeNode;
p->adjvex = j;
p->weight = w;
p->next = adjList[i].firstedge;
adjList[i].firstedge = p;
adjList[j].in++;
}
}
void GraphAdjList::BFSTraverse()//广度历遍算法
{
for (int i = 0; i < numVertexes; i++)
visited.push_back(false);
queue<int> Q;
EdgeNode* p;
for (int i = 0; i < numVertexes; i++)
{
if (!visited[i])
{
visited[i] = true;
cout << adjList[i].vert << " ";
Q.push(i);
while (!Q.empty())
{
i = Q.front();
Q.pop();
p = adjList[i].firstedge;
while (p)
{
if (!visited[p->adjvex])
{
visited[p->adjvex] = true;
cout << adjList[p->adjvex].vert << " ";
Q.push(p->adjvex);
}
p = p->next;
}
}
}
}
cout << endl;
}
bool GraphAdjList::TopologicalSort()//拓扑排序
{
stack<int>stack;
EdgeNode* e;
int count = 0, gettop;
for (int i = 0; i < numVertexes; i++)
{
if (0 == adjList[i].in)
stack.push(i);
}
for (int i = 0; i < numVertexes; i++)
etv.push_back(0);
while (stack.size())
{
gettop = stack.top();
stack.pop();
stack0.push(gettop);
cout << adjList[gettop].vert << " ";
count++;
for (e = adjList[gettop].firstedge; e; e = e->next)
{
if (!(--adjList[e->adjvex].in))
stack.push(e->adjvex);
if ((etv[gettop] + e->weight)>etv[e->adjvex])
etv[e->adjvex] = etv[gettop] + e->weight;
}
}
cout << endl;
if (count < numVertexes)
return true;
else
return false;
}
void GraphAdjList::Critica1Path()//求关键路径
{
EdgeNode* e;
int gettop,k;
int ete,lte;//活动最早发生时间和最迟发生时间
cout << "拓扑序列:" << endl;
TopologicalSort();
cout << "关键路径:" << endl;
for (int i = 0; i < numVertexes; i++)
ltv.push_back(etv[numVertexes - 1]);
while (stack0.size())
{
gettop = stack0.top();
stack0.pop();
for (e = adjList[gettop].firstedge; e; e = e->next)
{
k = e->adjvex;
if ((ltv[k] - e->weight) < ltv[gettop])
ltv[gettop] = ltv[k] - e->weight;
}
}
for (int i = 0; i < numVertexes; i++)
{
for (e = adjList[i].firstedge; e; e = e->next)
{
k = e->adjvex;
ete = etv[i];
lte = ltv[k] - e->weight;
if (ete == lte)
{
cout << "<" << adjList[i].vert << "," << adjList[k].vert << "> length: " << e->weight<<endl;
}
}
}
}
测试主代码:
#include <iostream>
#include "GraphAdjList.h"
using namespace std;
int main()
{
GraphAdjList G;
G.CreateALGraph();
G.Critica1Path();
system("pause");
return 0;
}
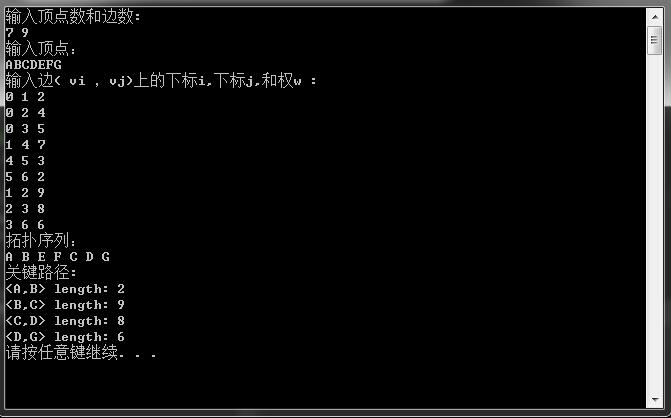
输入图1中的AOE图,在VS上运行结果如下:
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: