07、数据结构与算法C++：树-程序员江小北

树

前面我们介绍的数据结构都是一对一，但是我们经常需要面对一对多的问题。下面我们就来介绍下一对多的数据结构——树。

树( Tree )是n(n⩾0) n ( n ⩾ 0 ) 个结点的有限集。n=0 n = 0 时称为空树。在任意一棵非空树中: ( 1 )有且仅有一个特定的称为根 ( Root )的结点； (2) 当n>1 n > 1 时，其余结点可分为m(m>0) m ( m > 0 ) 个互不相交的有限集T1、T2、……、Tm T 1 、 T 2 、 … … 、 T m ,其中每一个集合本身又是一棵树，并且称为根的子树( SubTree )。

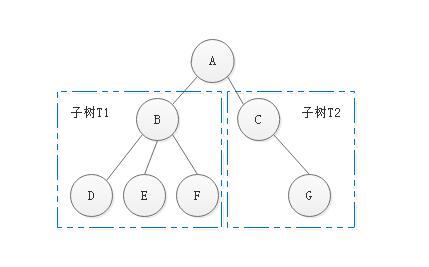
图1图 1

结点分类

结点拥有的子树数称为结点的度 (Degree) 。度为 0 的结点称为叶结点(Leaf) 或终端结点;度不为 0 的结点称为非终端结点或分支结点。除根结点之外，分支结点也称为内部结点。树的度是树内各结点的度的最大值。如图1，根节点是节点A；结点B、C是内部节点；结点D、E、F和G是叶结点。这棵树结点的度的最大值是结点B 的度，为 3 ，所以树的度也为 3 。

结点间关系

结点的子树的根称为该结点的孩子(Child) ，相应地，该结点称为孩子的双亲(Parent) 。同一个双亲的孩子之间直称兄弟 (Sibling)。结点的祖先是从根到该结点所经分支上的所有结点。以某结点为根的子树中的任一结点都称为该结点的子孙。

树的其他相关概念

结点的层次 ( LeveI) 从根开始定义起，根为第一层，根的孩子为第二层，以此类推。树中结点的最大层次称为树的深度 ( Depth)或高度。图1中的树的深度为3。双亲在同一层的结点互为堂兄弟。
如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为有序树，否则称为无序树。
森林 ( Forest) 是m(m⩾0) m ( m ⩾ 0 ) 棵互不相交的树的集合。

树的存储结构

树和线性表一样有顺序存储和链式存储两种结构。

双亲表示法

以一组连续空间存储树的结点，同时在每个结点中，附设一个指示器指示其双亲结点到链表中的位置。结点结构定义代码如下：

#define MAX_TREE_SIZE  100
class Node
{
   
     
public:
    char data;//结点数据
    int parent;//双亲位置

};
class Tree
{
   
     
    Node nodes[MAX_TREE_SIZE];
    int r, n;//根位置和结点数
};

根结点是没有双亲的，我们可以将它的位置域设置为-1。图1中的树采用双亲表示法可以如下表示：

下标	data	parent
0	A	-1
1	B	0
2	C	0
3	D	1
4	E	1
5	F	1
6	G	2

孩子表示法

我们可以把每个结点的孩子结点排列起来，以单链表作存储结构，则 n 个结点有 n 个孩子链表，如果是叶子结点则此单链表为空。然后 n 个头指针又组成一个线性表，采用顺序存储结构，存放进一个一维数组中。对于图1中的树可以如下图表示。

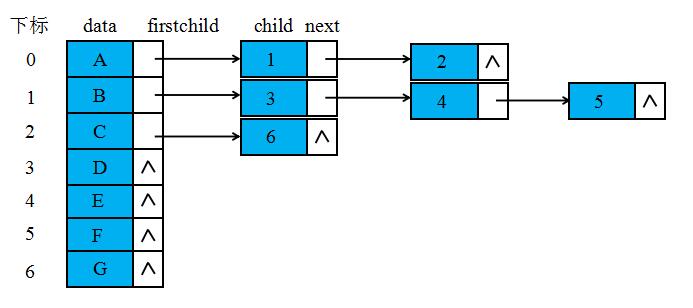
结点结构定义代码如下：

#define MAX_TREE_SIZE  100
class CTNode//孩子结点
{
public:
    int child;
    CTNode* next;
};
struct CTbox//表头结构
{
    char data;
    CTNode* firstchild;
};
class Tree//树结构
{
    CTbox nodes[MAX_TREE_SIZE];
    int r, n;//根位置和结点数
};

双亲孩子表示法

把双亲法和孩子法结合一起就是双亲孩子表示法。即在表头结构中加入双亲位置，结点结构定义代码如下：

#define MAX_TREE_SIZE  100
class CTNode//孩子结点
{
public:
    int child;
    CTNode* next;
};
struct CTbox//表头结构
{
    char data;
    int parent;//双亲位置
    CTNode* firstchild;
};
class Tree//树结构
{
    CTbox nodes[MAX_TREE_SIZE];
    int r, n;//根位置和结点数
};

孩子兄弟表示法

我们设置两个指针，分别指向该结点的第一个孩子和此结点的右兄弟。

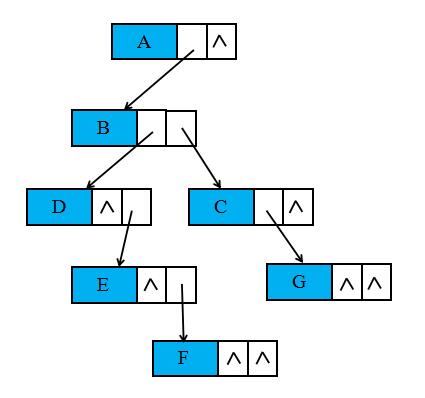
其结点结构定义代码如下：

class CSNode
{
   
     
private:
    char data;
    CSNode * firstchild, *rightsib;
};

这个表示法的最大好处是把一棵复杂的树变成了一棵二叉树。关于二叉树我们将在下一章中介绍。