12、数据结构与算法C++：拓扑排序-程序员快看-教程，程序员编程资料站

拓扑排序

在一个产品生成过程中，必须完成前一道的工序，才能进入下一道工序加工。像这样的工程我们可以用有向图来表示。

在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系，这样的有向图为顶点表示活动的网，我们称为AOV 网( Activity On VertexNetwork )。

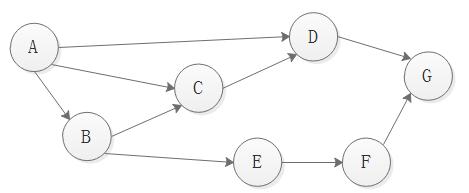
图1图 1

那什么又是拓扑排序呢？

设G=(V，E) G = ( V ， E ) 是一个具有n n 个顶点的有向图，V V 中的顶点序列v1,v2,...,vn v 1 , v 2 , . . . , v n ,满足若从顶点vi v i 到vj v j ，有一条路径，则在顶点序列中顶点vi v i ，必在顶点vj v j 之前。则我们称这样的顶点序列为一个拓扑序列。

对AOV 网进行拓扑排序的基本思路是: 从AOV 网中选择一个入度为0 的顶点输出，然后删去此顶点，井删除以此顶点为尾的弧，继续重复此步骤，直到输出全部顶点或者AOV 网中不存在入度为0 的顶点为止。相关代码如下：

#include<vector>
#define INFINITY 65535
using namespace std;
struct EdgeNode//边表结点
{
    int adjvex;//顶点下标
    int weight;//权值
    EdgeNode *next;//下一个结点
};
struct VertexNode//顶点表结点
{
    char vert;//顶点信息
    int in=0;//入度
    EdgeNode* firstedge;//边表头指针
};
class GraphAdjList
{
public:
    GraphAdjList();
    ~GraphAdjList();
    void CreateALGraph();//构建网图
    void BFSTraverse();//广度历遍算法
    bool TopologicalSort();//拓扑排序
private:
    vector<VertexNode> adjList;
    vector<bool> visited;//访问标志数组
    int numVertexes, numEdges;//顶点数、边数
};

#include "GraphAdjList.h"
#include<iostream>
#include<queue>
#include<stack>
using namespace std;

GraphAdjList::GraphAdjList()
{
}
GraphAdjList::~GraphAdjList()
{
}

void GraphAdjList::CreateALGraph()//构建网图
{
    int i, j, w;
    cout << "输入顶点数和边数:" << endl;
    cin >> numVertexes >> numEdges;
    cout << "输入顶点：" << endl;
    VertexNode vert;
    for (int k = 0; k < numVertexes; k++)
    {
        cin >> vert.vert;
        vert.firstedge = NULL;
        adjList.push_back(vert);
    }
    cout << "输入边( vi ，vj)上的下标i,下标j,和权w :" << endl;
    for (int k = 0; k < numEdges; k++)
    {
        cin >> i >> j >> w;
        EdgeNode *p = new EdgeNode;
        p->adjvex = j;
        p->weight = w;
        p->next = adjList[i].firstedge;
        adjList[i].firstedge = p;
        adjList[j].in++;
    }

}

void GraphAdjList::BFSTraverse()//广度历遍算法
{
    for (int i = 0; i < numVertexes; i++)
        visited.push_back(false);
    queue<int> Q;
    EdgeNode* p;
    for (int i = 0; i < numVertexes; i++)
    {
        if (!visited[i])
        {
            visited[i] = true;
            cout << adjList[i].vert << " ";
            Q.push(i);
            while (!Q.empty())
            {
                i = Q.front();
                Q.pop();
                p = adjList[i].firstedge;
                while (p)
                {
                    if (!visited[p->adjvex])
                    {
                        visited[p->adjvex] = true;
                        cout << adjList[p->adjvex].vert << " ";
                        Q.push(p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
    cout << endl;
}

bool GraphAdjList::TopologicalSort()//拓扑排序
{
    stack<int>stack;
    EdgeNode* e;
    int count = 0,gettop;
    for (int i = 0; i < numVertexes; i++)
    {

        if (0 == adjList[i].in)
            stack.push(i);
    }
    while (stack.size())
    {
        gettop = stack.top();
        stack.pop();
        cout << adjList[gettop].vert << "";
        count++;
        for (e = adjList[gettop].firstedge; e; e = e->next)
        {
            if (!(--adjList[e->adjvex].in))
                stack.push(e->adjvex);
        }
    }
    cout << endl;
    if (count < numVertexes)
        return true;
    else
        return false;

}

测试主程序：

#include <iostream>
#include "GraphAdjList.h"

using namespace std;

int main()
{
    GraphAdjList G;
    G.CreateALGraph();
    G.TopologicalSort();
    system("pause");
    return 0;
}

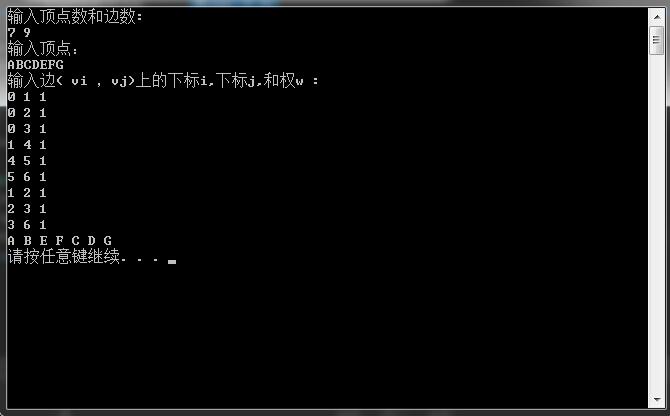
输入图1中的AOV网，在VS上运行结果如下：