学习笔记:数据结构与算法(十五):图的存储结构
-
- 邻接表(无向图)
- 邻接表(有向图)
- 邻接表(网)
- 十字链表
- 邻接多重表
- 边集数组
- 图的遍历
-
- 深度优先遍历
- 骑士周游问题
邻接表(无向图)
考虑将数组和链表结合在一起来存储,这种图结构称为邻接表。
处理方法:
1、 顶点用一个一维数组存储,当然也可以用单链表,但是数组更容易地读取顶点信息;
2、 图中每个顶点Vi的所有邻接点构成一个线性表,由于邻接点的个数不确定,所以选择用单链表存储;
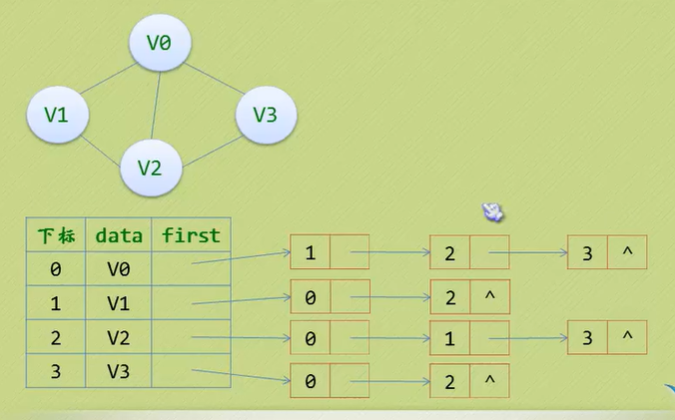
右侧单链表的数字代表数组中的位置,如果没有了就用空指针结束。
邻接表(有向图)
在有向图中,结构也是类似的,如下图所示
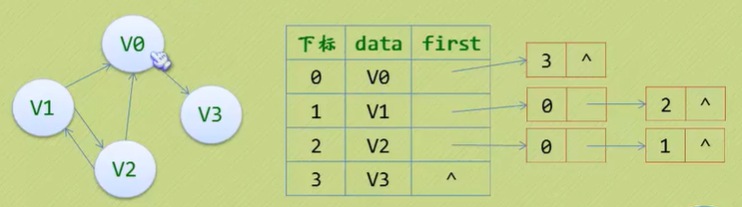
注意:要么表示出度要么表示入度。
邻接表(网)
对于带权值的网图,在边表结点定义中再增加一个数据域来存储权值。
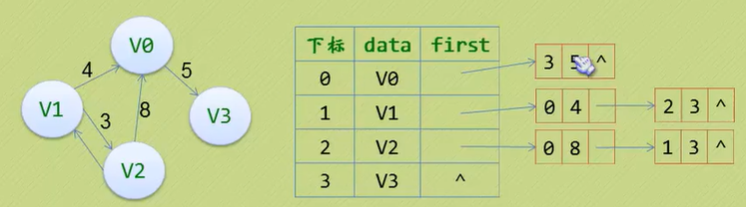
十字链表
重新定义顶点表结点结构

边表结点结构

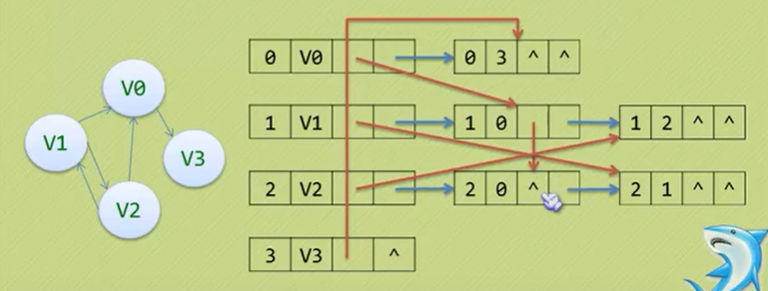
看V1这个结点,出度是1->0和1->2,所以在后面蓝色指出来了,入度是2->1,用红色的表示。
好处:把邻接表和逆邻接表整合在一起,容易找到为尾的弧,也容易找到头的弧。
缺点:结构复杂
邻接多重表
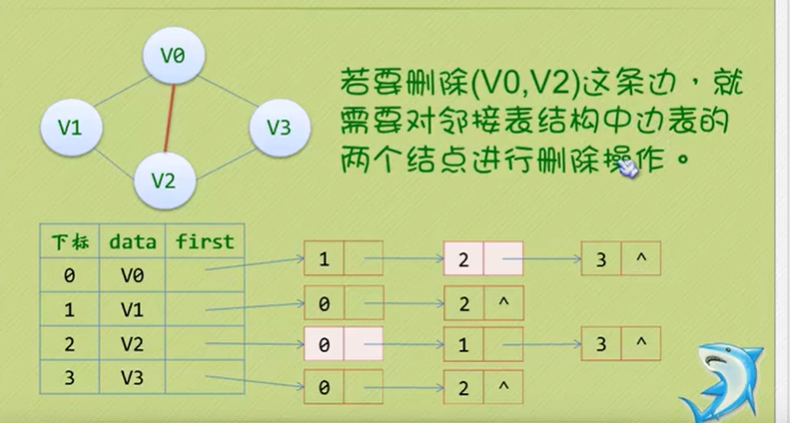
为了避免这种麻烦,可以对边表结构改装,重新定义,关注重点改为边而不是顶点

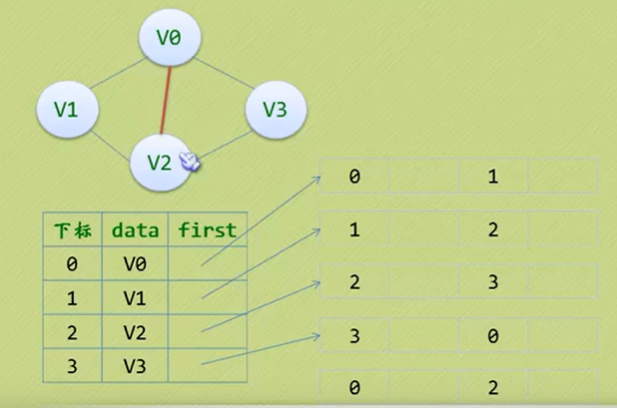
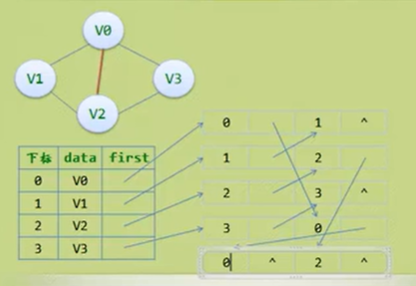
填充之后变为
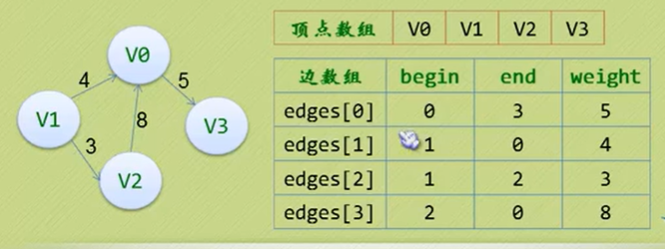
边集数组
两个一维数组构成,一个存储顶点的信息,另一个存储边的信息,边数组每个数据元素由一条边的起点下标,终点下标和权组成。
图的遍历
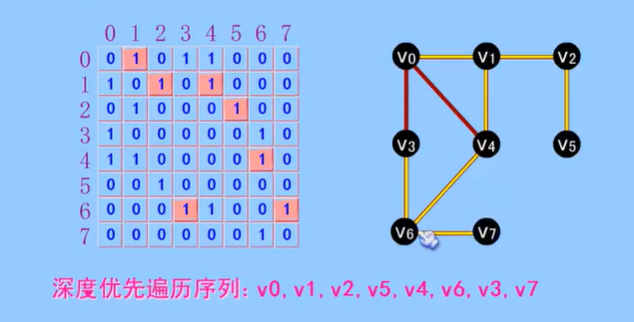
深度优先遍历
也称为深度优先搜索,简称为DFS。
骑士周游问题
国际象棋棋盘为8*8的方格棋盘,将“马”放在任意指定的方格中,按照走棋规则进行移动,要求每个方格只能进入一次,最终使得马走遍64个方格。
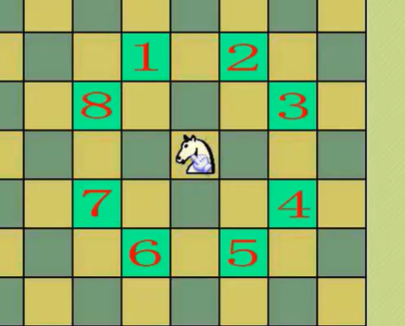
回溯法:一条路走到黑,碰到走过的结点就放弃再退回,和递归可以搭配使用
哈密尔顿路径:经过图G中每个顶点且只经过一次的一条轨迹。如果这个轨迹是一条闭合的路径,那么这条路径称为哈密尔顿回路。
#include <stdio.h>
#include <time.h>
#define X 8
#define Y 8
int chess[X][Y];
//找到基于xy位置的下一个可走的位置
int nextxy(int *x,int *y, int count)
{
switch(count)
case 0:
if(*x + 2 <= X -1 && *y - 1 >= 0 && chess[*x + 2][*y - 1] == 0)
{
*x += 2;
*y -= 1;
return 1;
}
break;
case 1:
if(*x + 2 <= X -1 && *y + 1 <=Y - 1 && chess[*x + 2][*y + 1] == 0)
{
*x += 2;
*y += 1;
return 1;
}
break;
case 2:
if(*x + 1 <= X -1 && *y -2>=0 && chess[*x + 1][*y-2] == 0)
{
*x += 1;
*y -= 2;
return 1;
}
break;
case 3:
if(*x + 1 <=X-1 && *y +2<=Y-1 && chess[*x + 1][*y + 2] == 0)
{
*x += 1;
*y += 2;
return 1;
}
break;
case 4:
if(*x -2>=0 && *y - 1 >=0 && chess[*x -2][*y-1] == 0)
{
*x -= 2;
*y -= 1;
return 1;
}
break;
case 5:
if(*x -2 <= X -1 && *y + 1 <=Y - 1 && chess[*x -2][*y + 1] == 0)
{
*x -= 2;
*y += 1;
return 1;
}
break;
case 6:
if(*x -1 >=0 && *y -2>=0 && chess[*x-1][*y-2] == 0)
{
*x -= 1;
*y -= 2;
return 1;
}
break;
case 7:
if(*x-1 >=0 && *y + 2 <=Y - 1 && chess[*x -1][*y + 2] == 0)
{
*x -= 1;
*y += 2;
return 1;
}
break;
default:
break;
}
return 0;
}
void print()
{
int i,j;
for(i=0;i<X;i++)
{
for(j=0;j<Y;j++)
{
printf("%2d\t",chess[i][j]);
}
printf("\n");
}
printf("\n");
}
//深度优先遍历棋盘,xy为位置坐标,tag是标记变量,走一步加一
int TravelChessBoard(int x,int y, int tag)
{
int x1 =x,y1=y,flag = 0,count = 0;
chess[x][y] = tag;
if(X*Y == tag)
{
//打印棋盘
print();
return 1 ;
}
//找下一个马的坐标,如果找到flag为1,否则为0
flag = nextxy(&x1,&y1,count);
while( 0 ==flag && count <7)
{
count++;
flag = nextxy(&x1,&y1,count);
}
while(flag)
{
if(TravelChessBoard(x1,y1,tag+1))
{
return 1;
}
//继续找到下一步可走的坐标
x1 =x;
y1 = y;
count ++;
flag = nextxy(&x1,&y1,count);
while( 0 ==flag && count <7)
{
count++;
flag = nextxy(&x1,&y1,count);
}
}
if( 0 == flag)
{
chess[x][y] = 0;
}
return 0;
}
int main()
{
int i,j;
clock_t start,finish;
start = clock();
for(i=0;i<X;i++)
{
for(j=0;j<Y;j++)
chess[i][j] = 0;
}
if(!TravelChessBoard(2,0,1))
{
printf("遍历失败!\n");
}
finish = clock();
printf("本次计算一共耗时:%f秒\n\n",(double)(finish - start)/CLOCKS_PER_SEC);
return 0;
}
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: