学习笔记:数据结构与算法(十三):赫夫曼树
- 赫夫曼树
-
- 定义
- 构造过程
- 名词解释
- 赫夫曼编码
赫夫曼树
定义
把两棵二叉树简化成叶子结点带权的二叉树(树结点间的连线相关的数叫做权)
结点的路径长度:从根结点到该结点的路径上的连接数
树的路径长度:树中每个叶子结点的路径长度之和
结点带权路径长度:结点的路径长度与结点权值的乘积
树的带权路径长度:树中所有叶子结点的带权路径长度之和。
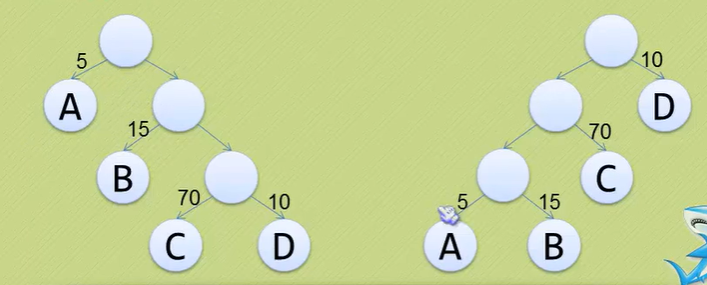
构造过程
1、 在森林中选出两棵根结点的权值最小的二叉树;
2、 合并选出的两个二叉树,新增加一个结点作为他俩的根,权值为二者之和;
3、 在森林里选出两棵根结点的权值最小的二叉树,进行合并;
4、 操作同2,重复3-2-3-2.;
名词解释
定长编码:像ASC*码
变长编码:单个编码的长度不一致,可以根据整体出现频率来调节。
前缀码:没有任何码字是其他码字的前缀
赫夫曼编码
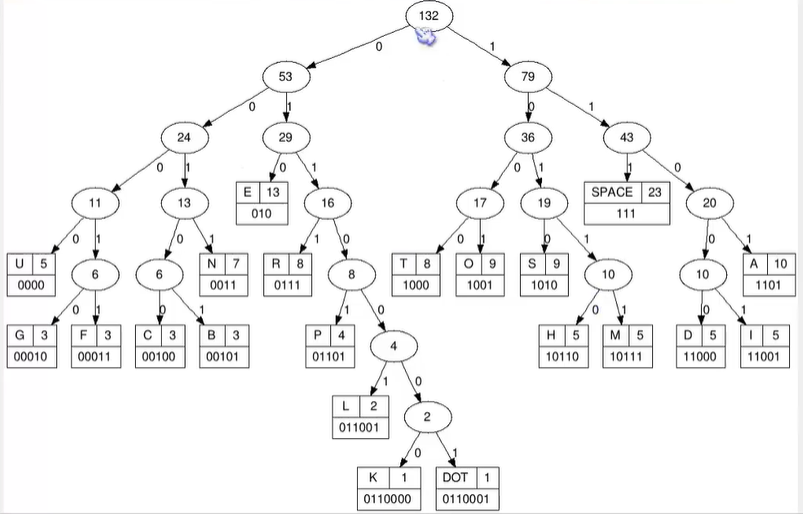
左子树用0来表示,右子树用1表示。圆圈里是结点的权值。
创建树之前,先创建一个具有优先级的队列,表示出现的次数,也就是权值。
代码可能没法放上来了,因为视频里没给完全
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: