学习笔记——数据结构与算法(二):数据结构和算法的复杂度
效率指的是算法的执行时间,算法执行的时间取决于:算法采用的策略、方案、编译产生的代码质量、问题的输入规模、己起执行指令的速度。因此,抛开硬件软件的问题,主要依赖于算法的好坏和输入规模。
算法时间复杂度
定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随着n的变化情况而确定T(n)的数量级,记作T(n)=O(f(n)),它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。
一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
推导大O阶方法
1、 用常数1取代运行时间中的所有加法常数;
2、 在修改后的运行次数函数中,只保留最高阶项;
3、 如果最高阶项存在且不是1,则去除与这个项相乘的常数;
4、 得到的最后结果就是大O阶;
线性阶
一般含有非嵌套循环涉及线性阶,随着问题规模n的扩大,对应计算次数呈直线增长。
例如
int i ,n = 100 , sum = 0;
for( i =0 ; i < n ; i++)
{
sum - sum + i ;
}
时间复杂度为O(n)
平方阶
嵌套的循环,两个嵌套就是O(n^2)
思考:如果是2n ^ 2+n/2呢,根据上述讲的方法,所以还是n^2
对数阶
2^x= n,则x = log(2)n,所以复杂度为O(logn)。
函数调用的时间复杂度分析
例题

分析:n++——一次,第二行:n ^ 2,第一个for循环同上,第二个for循环是n(n+1)/2,也是同上。所以就是3n^2 + 1,所以还是O(n ^ 2)
常见的时间复杂度
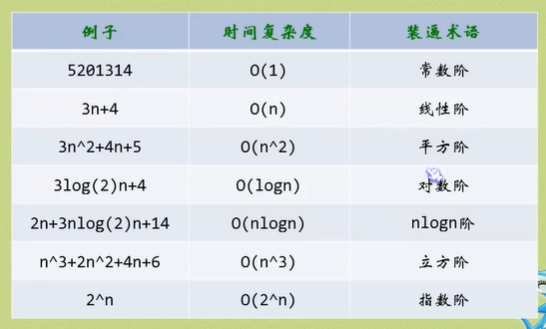
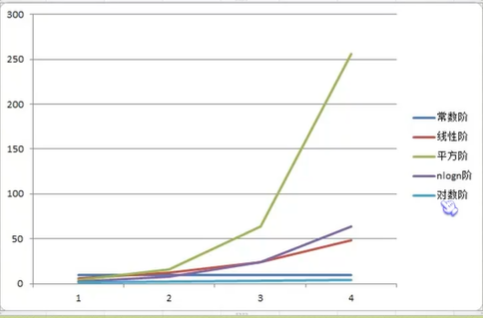
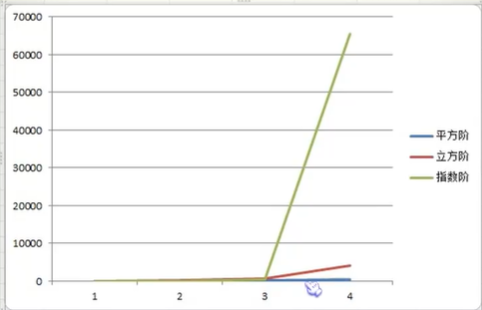
最坏情况与平均情况
算法分析时,例如随机数查找,有可能在第一个或者最后一个。
平均运行时间是期望的运行时间。
最坏运行时间是一种保证,提到的运行时间都是最坏情况的运行时间。
算法的空间复杂度
通过计算算法所需的存储空间实现,计算公式S(n) = O(f(n)),n为问题的规模。
通常,用时间复杂度来指运行时间的需求,用空间复杂度指空间需求。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: