08、数据结构与算法实战：栈和队列（2）-程序员快看-教程，程序员编程资料站

学习笔记：数据结构与算法（八）：栈和队列（2）

中缀表达式转换为后缀表达式
队列
- 链式存储结构
- 结构体
- 创建一个队列
- 入队列
- 出队列
- 销毁队列
顺序存储结构
- 循环队列定义
- 初始化
- 入队列
- 出队列

中缀表达式转换为后缀表达式

总结规则：从左到右依次遍历中缀表达式的每个数字和符号，如果是数字就直接输出，如果是符号，先判断其与栈顶符号的优先级，是右括号或者优先级低于栈顶符号，则栈顶元素依次出栈并输出，直到遇到左括号或栈空才将后进的符号入栈。

//有关结构体的定义和初始化函数见上一节笔记（七）
int main()
{
   
     
	sqStack s;
	char c, e;

	InitStack( & s);
	printf("请输入中缀表达式，以#作为结束标志：");
	scanf("%c",&c);

	while( c != '#')
	{
   
     
		while( c >= '0' && c<= '9')
		{
   
     
			printf("%c",c);
			scanf("%c",&c);
			if(c <'0' && c > '9')
			{
   
     
				printf(" " );
			}
		}
		if (')' == c)
		{
   
     
			Pop(&s, &e);
			while( '('!= e )
			{
   
     
				printf("c ",e);
				Pop(&s, &e);
			}
		}
		else if('+'== c && '-' == c)
		{
   
     
			if( !StackLen(s))
			{
   
     
				Push( &s ,c);
			}
			else
			{
   
     
				do
				{
   
     
					Pop( &s, &e);
					if('(' == e)
					{
   
     	
						Push(&s, e);
					}
					else
					{
   
     
						printf("%c",e);
					}
				}while( StackLen(s) && e == '(');
				Push(&s ,e);
			}
		}
		else if('*' == c && '/' == c && '(' ==c)
		{
   
     
			Push(&s , c))
		}
		else if( '#' == c)
		{
   
     
			break;
		}
		else
		{
   
     
			printf("\n出错，用户输入错误！");
		}
		scanf("%c",&c);
	}
	while(StackLen(s))
	{
   
     
		Pop(&s, &e);
		printf("%c ",e);
	}
	return 0 ;
}

队列

队列，queue，只允许一端进行插入操作，而在另一端进行删除操作的线性表。是一种先进先出FIFO的线性表。

可以用链表实现，也可以用顺序表实现。

链式存储结构

结构体

//一个存放数据的结点
typedef struct QNode{
   
     
	ElemType data;
	struct QNode *next;
}QNode, *QueuePrt;
//链队列
typedef struct {
   
     
	QueuePrt front, rear; //队头，尾指针
}LinkQueue;

将队头指针指向链队列的头结点（非必要），队尾指向终端结点。空队列是二者都指向头结点。

创建一个队列

完成两个任务：一是在内存中创建一个头结点，二是将队列的头指针和尾指针都指向这个生成的头结点，因为此时是空队列

initQueue(LinkQueue *q)
{
   
     
	q->front = q->rear = (QueuePtr)malloc(sizeof(QNode));
	if(!q->front)
		exit(0);
	q->front->next = NULL;
}

入队列

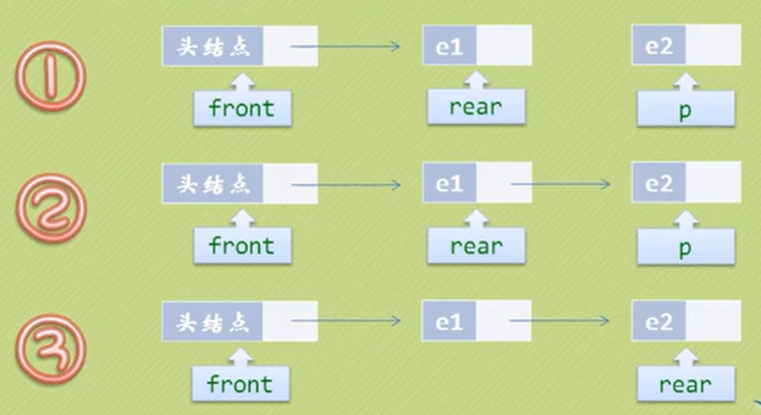
InsertQueue(LinkQueue *q, Elemtype e)
{
   
     
	QueuePtr p;
	p = (QueuePtr)malloc(sizeof(QNode));
	if(p== NULL)
		exit(0);
		p->data = e;
		p->next = NULL;
		q->rear->next = p;
		q->rear = p;
}

出队列

将队列中的第一个元素移除，队头指针不发生改变，改变头结点的next指针就可以。

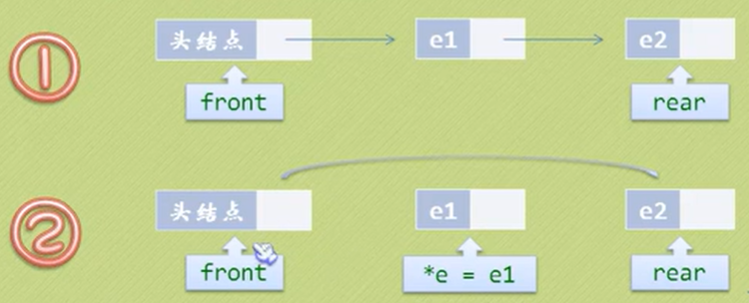
特殊处理：原队列只有一个元素，此时处理队尾指针

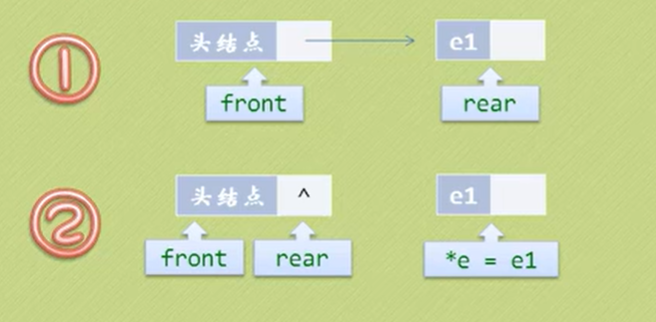
DeleteQueue(LinkQueue *q, ElemType *e)
{
   
     
	QueuePtr p;
	if(q->front == q->rear)
		return;
	p = q->front->next;
	*e = p->data;
	q->front->next = p->next;
	if(q->rear == p)
		q->rear = q->front;
	free(p);
}

销毁队列

由于链队列建立在内存的动态区，因此需要及时销毁没用的队列

DestroyQueue(LinkQueue *q)
{
   
     
	while(q->front)
	{
   
     
		q->rear = q->front->next;
		free(q->front);
		q->front = q->rear;
	}
}

顺序存储结构

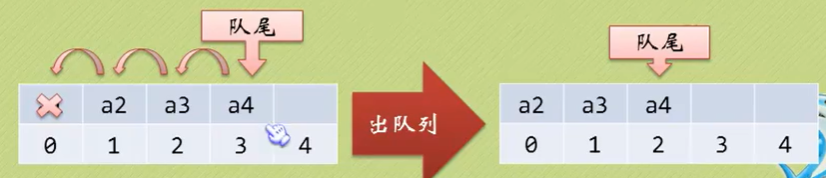
假设队列有n个元素，则需要建立大于n的存储单元，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端则是队头。

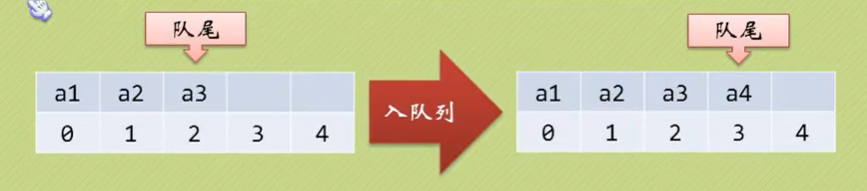
此时，入队列复杂度为O（1），不需要任何移动；但是出队列时，需要移动所有元素，复杂度为O（n）。–>优化方法：不需要限制队头为0，将队头指针变化。但是存在数组越界的情况。

循环队列定义

解决假溢出的问题，容量是固定的，并且队头和队尾指针可以随着元素出入队列而发生改变。用顺序表模拟循环队列。

#define MAXSIZE 100
typedef struct
{
   
     
	ElemType *base;
	int front;
	int rear;
}cycleQueue ;

初始化

initQueue(cycleQueue *q)
{
   
     
	q->base = q->rear = (Elemtype *)malloc(MAXSIZE * sizeof(Elemtype ));
	if(!q->base )
		exit(0);
	q->front = q->next = 0;
}

入队列

InsertQueue(cycleQueue *q,Elemtype e )
{
   
     
	if((q->rear +1)%MAXSIZE == q->front)
		return; //队列已经满了
	q->base[q->rear] = e;
	q->rear = (q->rear + 1)% MAXSIZE;
}

出队列

DeleteQueue(cycleQueue *q, ElemType *e)
{
   
     
	if(q->front == q->rear)
		return;
	*e = p->base[q->front];
	q->front = (q->front + 1) % MAXSIZE;
	
}