34、数据结构与算法C：算法套佛洛伊德算法-程序员快看-教程，程序员编程资料站

前言

佛洛伊德算法和迪杰斯特拉算法非常像，但是它求的是任何一个点到其他点之间的距离。

假设有一张图:

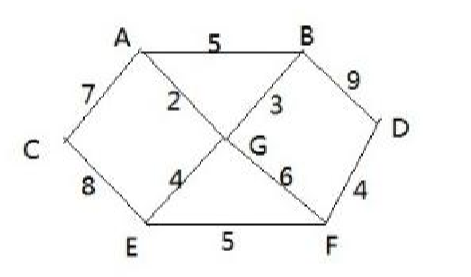
转换为矩阵为:

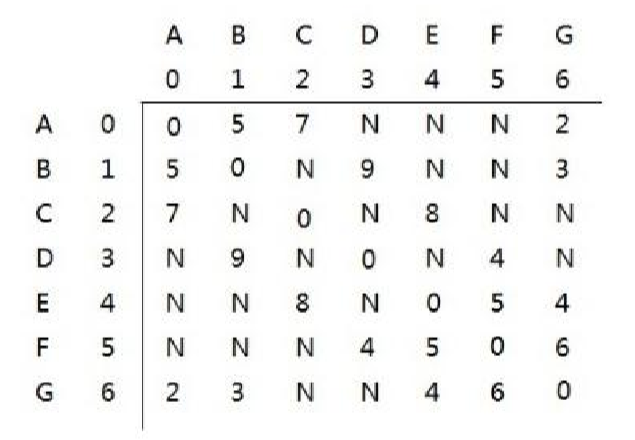
他们的前驱为:

可能上面表述前驱不清楚，举个例子。

看下图:

这第二种图表示，从A 经过A 到B，B点的前驱是A，他们的长度是5，红框中的数表示是A经过的点。

现在A到不了D，A经过A到D就是N，表示无限大。

所以我们需要更新数据，得到最优解。

解法如下:

举个例子，原始图是A通过A到B的距离。

那么可以尝试这样，让所以的点经过A到达其他的点，他们的距离是否更短。如图:

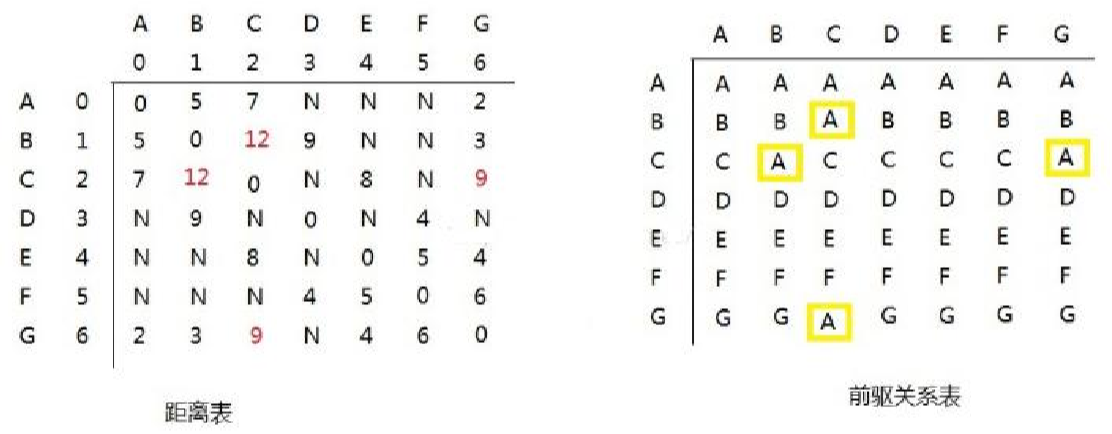
以此类推其他。

正文

代码:

static void Main(string[] args)
{
	// 测试看看图是否创建成功
	char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
	//创建邻接矩阵
	int N = 65535;
	int[,] matrix = {
	  { 0, 5, 7, N, N, N, 2 },
	  { 5, 0, N, 9, N, N, 3 },
	  { 7, N, 0, N, 8, N, N },
	  { N, 9, N, 0, N, 4, N },
	  { N, N, 8, N, 0, 5, 4 },
	  { N, N, N, 4, 5, 0, 6 },
	  { 2, 3, N, N, 4, 6, 0 }};
	GraphFoy graph = new GraphFoy(matrix, vertex);
	graph.floyd();
	graph.show();
	Console.Read();
}
}
class GraphFoy {
private char[] vertex;
private int[,] dis;
private int[,] pre;
public GraphFoy(int[,] matrix,char[] vertex)
{
	this.vertex = vertex;
	this.dis = matrix;
	this.pre = new int[vertex.Length,vertex.Length];
	for (int i=0;i<vertex.Length;i++)
	{
		for (int j=0;j<vertex.Length;j++)
		{
			this.pre[i, j] = i;
		}
	}
}
// 显示pre数组和dis数组
public void show()
{
	//为了显示便于阅读，我们优化一下输出
	char[] vertex = { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
	for (int k = 0; k < vertex.Length; k++)
	{
		// 先将pre数组输出的一行
		for (int i = 0; i < vertex.Length; i++)
		{
			Console.Write(vertex[pre[k,i]] + " ");
		}
		Console.WriteLine();
		// 输出dis数组的一行数据
		for (int i = 0; i < vertex.Length; i++)
		{
			Console.Write("(" + vertex[k] + "到" + vertex[i] + "的最短路径是" + dis[k,i] + ") ");
		}
		Console.WriteLine();
	}
}

public void floyd()
{
	int len = 0;
	for (int k = 0; k < vertex.Length; k++)
	{
		for (int i = 0; i < vertex.Length; i++)
		{
			for (int j = 0; j < vertex.Length; j++)
			{
				len = dis[k, i] + dis[k, j];
				if (len<dis[i,j])
				{
					dis[i, j] = len;
					pre[i, j] = pre[k, j];
					//pre[i,j]=pre[k,j];
				}
			}
		}
	}
}

结果如下: