12、数据结构与算法C：图的深度遍历和广度遍历-程序员快看-教程，程序员编程资料站

前言

简介图:

在数据的逻辑结构D=（KR）中，如果K中结点对于关系R的前趋和后继的个数不加限制，即仅含一种任意的关系，则称这种数据结构为图形结构。

来源百度百科

图形结构是一种比树形结构更复杂的非线性结构。在树形结构中，结点间具有分支层次关系，每一层上的结点只能和上一层中的至多一个结点相关，但可能和下一层的多个结点相关。而在图形结构中，任意两个结点之间都可能相关，即结点之间的邻接关系可以是任意的

然后就是盗图阶段:

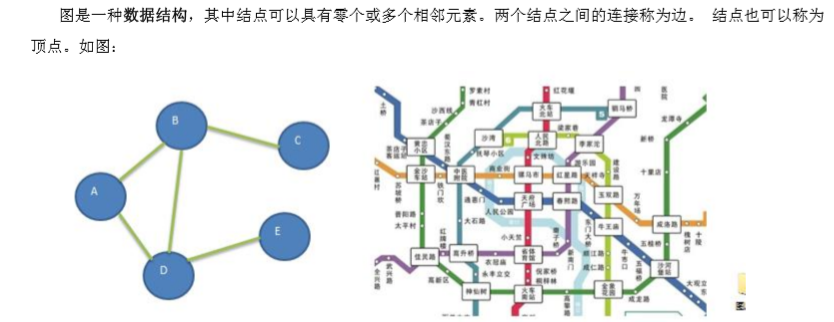
后面就是一些基础常识，我找到一个比较全的:

https://www.cnblogs.com/songgj/p/9107797.html

正文

那么就来看一下图的深度遍历和广度遍历吧。

先来定义一个图:

public class Graph
{
	private List<String> vertexList; //存储顶点集合
	private int[,] edges; //存储图对应的邻结矩阵
	private Boolean[] isVisited;// 判断是否访问了
	int numOfEdges;
	public Graph(int n){
		vertexList = new List<string>();
		edges = new int[8, 8];
		isVisited = new Boolean[8];
	}
	/// <summary>
	/// 增加节点
	/// </summary>
	/// <param name="vertex">节点</param>
	public void addVertex(string vertex)
	{
		vertexList.Add(vertex);
	}
	public void insertEdge(int x,int y,int weight)
	{
		//增加他们的连线 且设置他们的权重
		edges[x, y] = 1;
		edges[y, x] = 1;
		numOfEdges++;
	}

	public void showEdges()
	{
		for (int i=0;i< isVisited.Length;i++)
		{
			for (int j = 0; j < isVisited.Length; j++)
			{
				Console.Write(edges[i,j]+"  ");
			}
			Console.WriteLine();
		}
	}
}

测试一下:

String[] Vertexs = { "1", "2", "3", "4", "5", "6", "7", "8" };
//创建图对象
Graph graph = new Graph(Vertexs.Count());
//循环的添加顶点
foreach (String vertex in Vertexs)
{
	graph.addVertex(vertex);
}
//更新边的关系
graph.insertEdge(0, 1, 1);
graph.insertEdge(0, 2, 1);
graph.insertEdge(1, 3, 1);
graph.insertEdge(1, 4, 1);
graph.insertEdge(3, 7, 1);
graph.insertEdge(4, 7, 1);
graph.insertEdge(2, 5, 1);
graph.insertEdge(2, 6, 1);
graph.insertEdge(5, 6, 1);
graph.showEdges();
Console.ReadKey();

结果:

这么看可能不清晰哈，那么我画个图，看一下。

这是下面这张图哈:

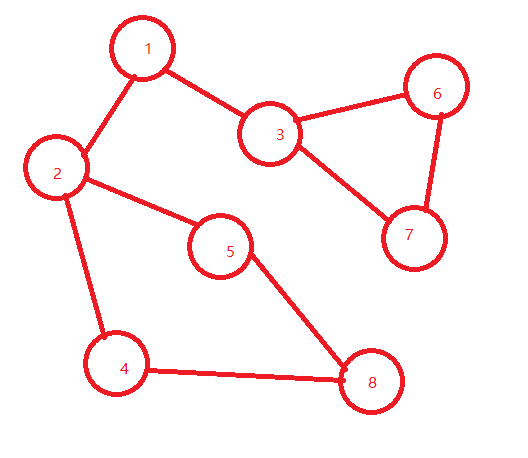
深度遍历:

private int getFirstNeighbor(int index)
{
	for (int j = 0; j < isVisited.Length; j++)
	{
		if (edges[index, j] > 0)
		{
			return j;
		}
	}
	return -1;
}
/// <summary>
/// 通过邻接节点来获取下一个节点
/// </summary>
/// <param name="v1"></param>
/// <param name="v2"></param>
/// <returns></returns>
public int getNextNeighbor(int v1, int v2)
{
	for (int j = v2+1; j < isVisited.Length; j++)
	{
		if (edges[v1, j] > 0)
		{
			return j;
		}
	}
	return -1;
}
/// <summary>
/// 深度遍历
/// </summary>
/// <param name="i"></param>
public void dfs(int i)
{
	//打印遍历的值
	Console.Write(vertexList[i]+"  ");
	isVisited[i] = true;
	int w = getFirstNeighbor(i);
	while (w != -1)
	{
		if (!isVisited[w])
		{
			dfs(w);
		}
		w = getNextNeighbor(i,w);
	}
}

然后调用函数:

 graph.dfs(0);

得到的结果是:

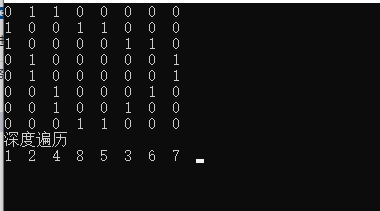
看下广度遍历吧:

//对一个结点进行广度优先遍历的方法
public void bfs(int i)
{
	//打印遍历的值
	Console.Write(vertexList[i] + "  ");
	LinkedList<int> queue = new LinkedList<int>();
	queue.AddLast(i);
	int u;
	while (queue.Count != 0)
	{
		u = queue.First.Value;
		queue.RemoveFirst();
		int w = getFirstNeighbor(i);
		while (w != -1)
		{
			if (!isVisited[w])
			{
				Console.Write(vertexList[w] + "  ");
				isVisited[w] = true;
				queue.AddLast(w);
			}
			w = getNextNeighbor(u, w);
		}
	}
}

然后调用:

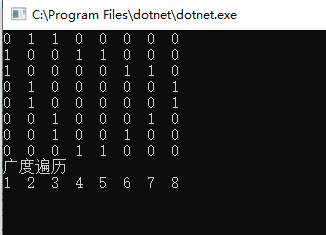
Console.WriteLine("广度遍历");
graph.bfs(0);

结果: