31、数据结构与算法C：算法套路普利姆算法-程序员快看-教程，程序员编程资料站

前言

看一个题目:

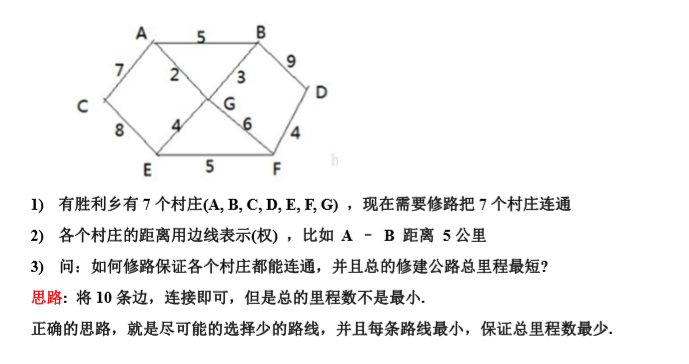
这个问题就是求最小生成树，是图转换为树的一种方式。

最小生成树概念:

最小生成树简称MST。

1、 n个顶点，一定有n-1条边；

2、包含全部顶点；

3、图转换为最小生成树，权重之和最小；

解题思路:

1、假设从a开始为顶点，找到和a相接的最小边；
2、在图中和a相接的是G，那么选择条然后找到和A、G相接的最小边，是BG，然后选择BG这条边；
3、以此类推；

正文

代码:

static void Main(string[] args)
{
	char[] data = new char[] { 'A', 'B', 'C', 'D', 'E', 'F', 'G' };
	int verxs = data.Length;
	//邻接矩阵的关系使用二维数组表示,10000这个大数，表示两个点不联通
	int[,] weight = new int[,]{
	{10000,5,7,10000,10000,10000,2},
	{5,10000,10000,9,10000,10000,3},
	{7,10000,10000,10000,8,10000,10000},
	{10000,9,10000,10000,10000,4,10000},
	{10000,10000,8,10000,10000,5,4},
	{10000,10000,10000,4,5,10000,6},
	{2,3,10000,10000,4,6,10000},};
	//创建要修的路,初始化节点的个数
	MGraph mGraph = new MGraph(verxs);
	//创建一个MinTree对象
	MinTree minTree = new MinTree();
	minTree.createGraph(mGraph, verxs, data, weight);
	Console.WriteLine("显示原始图");
	minTree.showGraph(mGraph);
	var newGraph=minTree.prim(mGraph, 0);
	Console.WriteLine("显示最小生成树图");
	minTree.showGraph(newGraph);
	Console.Read();
} 
}

class MinTree {
//不污染数据
public void createGraph(MGraph mGraph, int verxs, char[] data, int[,] weight)
{
	for (int i = 0; i < verxs; i++)
	{
		mGraph.data[i] = data[i];
		for (int j = 0; j < verxs; j++)
		{
			mGraph.weight[i,j] = weight[i,j];
		}
	}
}
//遍历图
public void showGraph(MGraph mGraph)
{
	for (int i=0;i<mGraph.verxs;i++)
	{
		for (int j = 0; j < mGraph.verxs; j++)
		{
			Console.Write(mGraph.weight[i,j]+"  ");
		}
		Console.WriteLine();
	}
}

/// <summary>
/// 图转树核心算法
/// </summary>
/// <param name="mGraph">原始图</param>
/// <param name="v">初始化访问节点</param>
public MGraph prim(MGraph mGraph,int v)
{
	int[] isVisited = new int[mGraph.verxs];
	isVisited[v] = 1;
	int y = -1;//y为数组竖轴
	int x = -1;//x为数组横轴
	MGraph newGraph = new MGraph(mGraph.verxs);
	newGraph.data = (char[])mGraph.data.Clone();
	int minWeight = 1000;
	//一共要计算出verxs-1条边
	for (int k=1;k<mGraph.verxs;k++)
	{
		for (int i=0;i<mGraph.verxs;i++)
		{
			for (int j = 0; j < mGraph.verxs ; j++)
			{
				if (isVisited[i] == 1 && isVisited[j] == 0 && mGraph.weight[i, j] < minWeight)
				{
					y = i;
					x = j;
					minWeight = mGraph.weight[i, j];
				}
			}
		}
		Console.WriteLine("在"+mGraph.data[y]+"和"+ mGraph.data[x]+"之间修了一条权重为"+minWeight+"的路");
		newGraph.weight[y,x] = minWeight;
		isVisited[x] = 1;
		minWeight = 1000;
	}
	return newGraph;
}
}

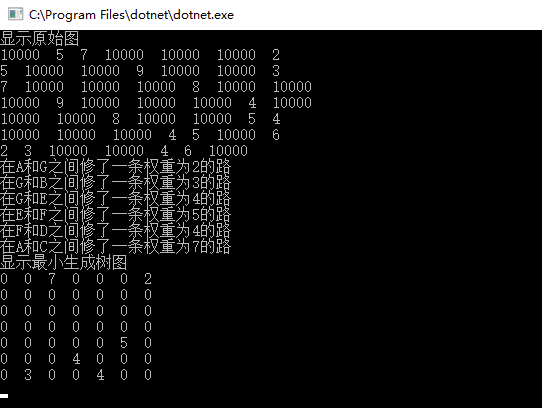
结果: