摘要
二叉搜索树的特性-节点的左侧部分比它小,右侧部分比它大,使得二叉搜索树在查找节点有二分法的效果,也提高了它的添加和删除处理,毕竟添加和删除也是先查找位置,然后再处理。
平衡二叉搜索树就是持续保证这样的高效性,进入正题:
二叉搜索树在添加或者删除的过程中,在一些场景下退化为链表,比如对比一组数据:7、4、9、2、5、8、11。按照现在的顺序添加和按照数据的大小依次添加的结果:
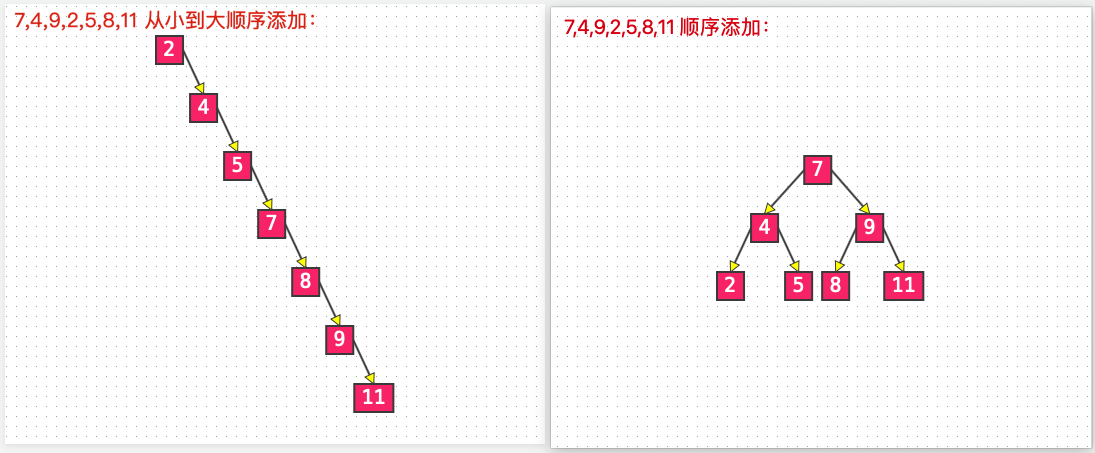
当数据已经有顺序,使用二叉搜索树添加就会变成一个线性链表,这是我们不愿意看到的结果。
同理,在删除节点的时候,也是容易多次删除之后的二叉搜索树也会是一个线性链表。
所以就引入平衡二叉搜索树来避免退化成线性表的问题。
平衡
二叉搜索树节点数量确定不变的情况下,左右子树的高度越接近,这个二叉搜索树就越平衡。最理想的平衡就是左右子树的高度差为 0 或 1,比如满二叉树或完全二叉树。
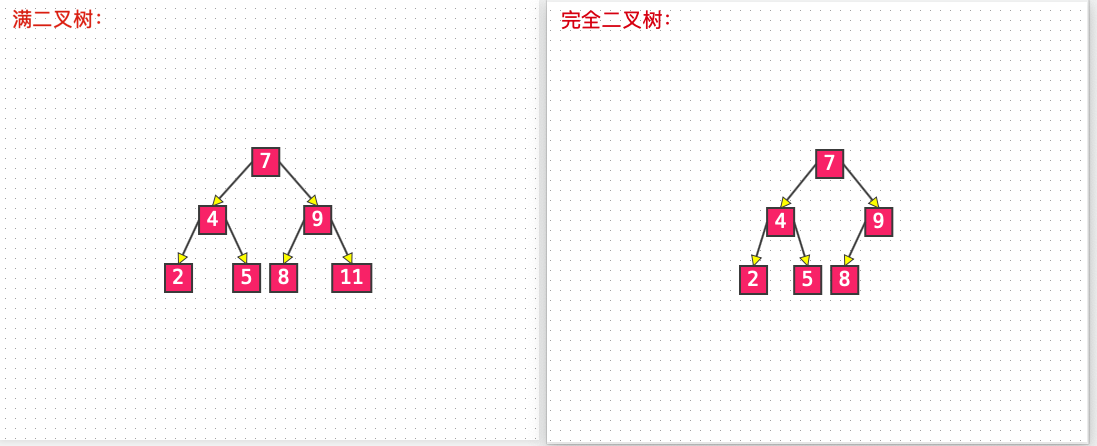
如何平衡?
添加节点或者删除节点是不能限制,也就是不能控制二叉搜索树的节点数量。所以只能在添加或者删除之后去调整二叉搜索树的高度,达到平衡。
若要达到理想中的平衡(比如完全二叉树),也是没有问题的,就是增加调整的次数的处理。但是凡事都要有个度,调整的次数多了,反而会增加时间复杂度。所以调整到平衡的原则就是用尽量少的调整次数达到适度平衡就好,这样达到适度平衡的二叉搜索树,也叫做平衡二叉搜索树。
平衡二叉搜索树
平衡二叉搜索树,英文为 Balanced Binary Search Tree,简称 BBST。比较经典的平衡二叉搜索树有AVL 树和红黑树。这里先简单介绍,平衡二叉搜索树逻辑和细节很多,后在接下来分很多期来说明。
AVL 树
AVL树命名是根据它的两位发明者名称得来,是相对很早发明的自平衡搜索树之一。
AVL树引入平衡因子的概念,平衡因子为某个节点的左右子树的高度差。每个节点的平衡因子只可能是 1、0、-1,当超过这个范围就是失衡。
红黑树
红黑树也是自平衡的二叉搜索树,它的节点只有红色或者黑色,并且根节点是黑色,叶子节点是红色,红色节点的子节点必须是黑色,父节点也必须是黑色。
这些规则构成整个红黑树。
AVL 树和红黑树被应用到很多场景,是数据结构中基础并且重要的部分。很多优秀的数据结构或者算法基于它实现或者借鉴它的思路。很值得花费精力去弄懂它。
版权声明:本文不是「本站」原创文章,版权归原作者所有 | 原文地址: